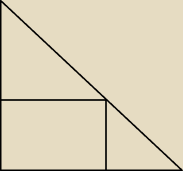
 W trójkat prostokątny o przyprostokątnych 6cm i 8 cm wpisujemy prostokąty, w taki
sposób, jak na rysunku obok. Wyznacz wymiary tego prostokąta, który ma największe pole
powierzchni.
W trójkat prostokątny o przyprostokątnych 6cm i 8 cm wpisujemy prostokąty, w taki
sposób, jak na rysunku obok. Wyznacz wymiary tego prostokąta, który ma największe pole
powierzchni.
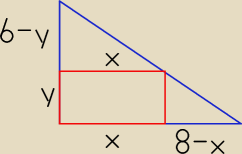
| 6 − y | 6 | |||
Z podobieństwa trójkątów otrzymujemy proporcję: | = | |||
| x | 8 |
| 4 | ||
Stąd x = | (6 − y) | |
| 3 |
| 4 | ||
Pole prostokąta P = x*y => P = | (6 − y) * y | |
| 3 |
| 4 | ||
P = 8y − | y2 | |
| 3 |
| 4 | ||
Otrzymaliśmy funkcję kwadratową P(y) = − | y2 + 8y, której wykresem jest | |
| 3 |
| −8 | 3 | −24 | |||||||||||||
dla y = | * | = | = 3 | ||||||||||||
| 3 | −8 |
| 4 | ||
x = | (6 − 3) = 4 | |
| 3 |
 bo tego
nie czaję
bo tego
nie czaję
| 6 − y | 6 | |||
podobieństwo trójkątów i proporcja | = | |||
| x | 8 |