kilka zadań z geometrii-pola słaba z matmy...;(: Zad1 Na sześciokącie foremnym opisanookrag i w ten sześciokąt wpisano okrąg. Pole powstałego pierścienia wynosi 2π. Oblicz pole sześciokąta Zad2 Stosunek pola rombu do pola koła wpisanego w ten romb wynosi 8:π. Oblicz miarę kąta ostrego tego rombu. Zad.3 Dłuższa przekątna rombu ma długośc d a kat ostry rombu ma miarę 60 stopni. Oblicz stosunek pola kołą wpisanego w ten romb do pola tego rombu.

tim: Pomagam I.

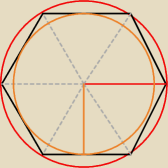
tim: R koła opisanego na (czerwony) = bokowi = a

	a√3
r koła wpisanego w (pomarańczowy) = htrójkąta równobocznego o boku a =
	2

Pole koła o promieniu R − Pole koła o promieniu r = Pole pierścienia = 2π πR² − πr² =2π π(R² − r²) = 2π /π R² − r² = 2

	a√3
a2 −		2 = 2
	2

	3
a2 −		a2 = 2
	4

1
	a2 = 2
4

a² = 8 a = √8 = 2√2 Mamy bok. Teraz liczymy pole sześciokąta...

	a2√3
Wzór to pole sześciu trójkątów równobocznych o boku a = 6 *
	4

słaba z matmy...;(: Dzięki, a resztę też rozumiesz?

tim: Pomogę też drugie

kłopoty z matematyką: Dziękuję, może wkońcu coś zrozumię

kłopoty z matematyką: Nie ma to jak mało co czaić, i prosić o pomoc na forach...

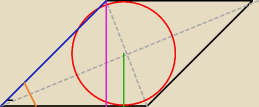
tim: r koła wpisanego w romb = 0,5 wysokości tego rombu. Pole rombu = a * h

	1
Pole koła wpisanego w romb = πr2 = π(		h)2
	2

Przyrównujemy.

a * h		8
	=
1   π( h)2   2		π

Proporcja.

	1
a * h * π = 8 * π*		h2 /:π
	4

ah = 2h² /:h a = 2h Liczymy. h = różowe, a = niebieskie

	h		1
Liczymy sin α =		=
	2h		2

α = 30^O

tim: Jka czegoś nie teges to pisz.

kłopoty z matematyką: Nie, dokąłdnie tłumaczysz i trochę mi się rozjaśnia

kłopoty z matematyką: Jeszzce jakbyś to trzecie tak dokłądnie wytłumaczył to Niech Ci będą serdeczne dzięki

tim: Masz może do trzeciego odp?

tim: Dobra wyszedł dziwny wynik ale rozwiązuje

tim: METODA 1! P_rombu = a * h

	1
Pkoła = π(		h)2
	2

	a√3
z sin 60 liczymy stosunek h / a, który wynosi √3 / 2 ⇒ h =
	2

Stosunek P_r / P_k

a * h
	=
1   π( h)2   2

a√3   a *   2
	=
1   π h2   4

a2√3   2
	=
1   a√3   π ( )2   4   2

a2√3   2
	=
1 3a2   π   4 4

a2√3   2
	=
3a2   π   16

a2√3   2
	=
3a2   π   16

a2√3		16		8√3
	*		=
2		3a2π		3π

tim: Metoda 2.! P_r = 2a * r = a² * sinα

	√3
2ar = a2		/:a
	2

	a√3
2r =
	2

	a√3
r =
	4

Podstawiam do wzoru na pole koła.

	a√3		3a2
πr2 = π(		)2 =		π
	4		16

	a√3
2ar =
	2

Dalej jak w pierwszym.. stosunek itd.

kłopoty z matematyką: ojć, nie czaję końcówki zadania 2, liczenie tego sinusa...

kłopoty z matematyką: Nie, spoko, już mam

kłopoty z matematyką: Kurde, a jak to 3 złożyć by to d było użyte? Bo ono jest podane i być musi