planimetria-maturalne kamil: promien okregu wpisanego w trojkat prostokatny jest rowny r, a jeden z katow ostrych ma miere α. wyznacz pole tego trojkata.

xpt: pomagam

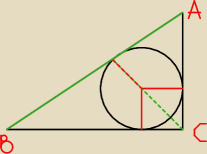
xpt: czerwone kreski − promień koła czerwono czarna linia − odcinek równy r linia czerwono zielona − znowu r ;P zielona przerywana: − cała to wysokość h_c − tylko zielona to przekątna kwadratu o boku r h_c można łatwo obliczyć, jest to r + r√2 Bierzemy 2 wzory na pole trójkąta i je porównujemy

	1
P=		c*hc (to jest dla dowolnego trójkąta wzór)
	2

	1
P=		c2sin2α (to wzór dla trójkąta prostokątnego)
	4

1		1		2
	c*hc=		c2sin2α mnożymy razy
2		4		c

	1
hc=		csin2α
	2

wyznaczamy c

	2hc
c=
	sin2α

Podstawiamy za h_c i za c wyliczone wartości, a nastepnie podstawiamy do wzoru

	1		(r+r√2)2
P=		c*Hc =
	2		sin2α

za sin2α podstawiamy 2sinαcosα

	1		(r+r√2)2
P=		c*Hc =
	2		2sinαcosα

xpt: zaraz − ale błąd zrobiłem :P ZADANIE ROZWIĄZANE ŹLE Jak by wysokośc sie pokrywała z r to to by był trójkąt prostokątny równoramienny. Zaraz coś wymyślę i dla dowolnego prostokątnego postaram się zrobić

kamil: a skad zabrales ten wzor na pole tr prostkatnego? mozesz mi wytlumaczyc jak do mnie doszedles?

kamil: spoko

kamil: juz chyba mam. tylko zastanawia mnie jedna rezcz czy tg^β₂=ctg^α₂

xpt: Znalazłem pewno wyjście z sytuacji, ale wynik (powinien byc poprawny) ne wygląda zachęcająco :) Najpierw liczę h_c Biorę 2 wzory na pole

	2P
P=pr ⇒ r=
	a+b+c

	2P
P=½ chc ⇒ hc=
	c

dzielę h_c przez r, a następnie mnożę razy r (niby nielogiczne, ale jednak coś w tym jest)

	2P		2P		a+b+c
hc = hc : r * r		:		* r =		*r =
	c		a+b+c		c

	a		b
= (		+		+ 1) *r = (cosα+sinα+1)*r
	c		c

teraz liczę c (tak samo jak poprzednim razem biorę 2 wzory na pole

	1		1
P=		chc i P=		c2sin2α
	2		4

1		1
	chc =		c2sin2α mnoże obustronnie *2
2		4

	1
chc =		csin2α dzielę obustronnie :2
	2

	1		2
hc =		csin2α mnoże obustronnie *
	2		2sinα

	2hc
c=
	csin2α

(cosα+sinα+1)*r Podstawiam do wzoru P=½ch_c

	2((cosα+sinα+1)*r)
P=½		* (cosα+sinα+1)*r =
	csin2α

	[(cosα+sinα+1)*r]2
	sin2α

xpt: na koncu jak jest sin2α top trzeba zamienić na 2sinαcosα, bo nie mamy kąta 2α tylko kąt α ;)

kamil: wyniki jak powinien wyjsc to r²(tg^α₂+1)(tg(45−^α₂)+1) P= −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− tg(45−^α₂)

Mickej : zadko kiedy wyjdzie ci taki sam wynik w tego typu zadaniach

xpt: kamil − wynioki sa różne czy tylko ich postaci?

Bogdan: Proponuję następujące rozwiązanie: α − miara kata przy wierzchołku A. a, b − długości przyprostokątnych, c − długość przeciwprostokątnej p − połowa długości obwodu trójkąta a = csinα, b = ccosα,

	1		2r
r =		(a + b − c) => 2r = c(sinα + cosα − 1) => c =
	2		sinα + cosα − 1

	1		1
p =		(a + b + c) => p =		c(sinα + cosα + 1)
	2		2

	(sinα + cosα + 1)
p =
	sinα + cosα − 1

	(sinα + cosα + 1)
Pole trójkąta P = pr => P = r *
	sinα + cosα − 1