dwusieczna kąta KATALKA: POMÓŻCIE Wykaż, że dwusieczna kąta wewnętrznego dowolnego trójkąta dzieli bok przeciwległy w stosunku do pozostałych boków.

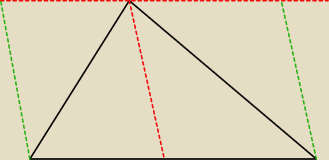
Skipper: ... można np. tak−

KATALKA: mógłbyś mi wytłumaczyc na czym tak w ogóle ten dowód polega? z góry dziękuję

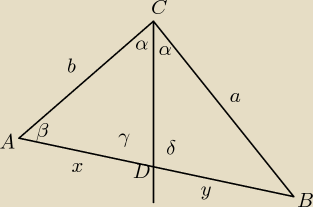
ArtuśPati: zał.: |CD| jest dwusieczna kąta ACB,

	b		x
teza :		=
	a		y

d−d: obliczamy katy γ=180−α−β sinγ=sin(180−α−β) = sin(α+β) δ=α+β sinδ=sin(α+β) Zapisujemy twierdzenie sinusow dla bokow a,x,y ∧ b

b		x		a		y
	=		∧		=
sin(α+β)		sinα		sin(α+β)		sinα

sinα		x		sinα		y
	=		∧		=
sin(α+β)		b		sin(α+β)		a

	x		y
Po podstawieniu otrzymujemy		=		po drobnym przeksztalceniu otrzymamy
	b		a

	a		y
		=		cnd.
	b		x

ArtuśPati: @skiper no chyba nie. Aczkolwiek mozesz mi wytlumaczyc swoj tok myslenia

Skipper: powstałe równoległoboki są podobne za zasadzie identycznych kątów −

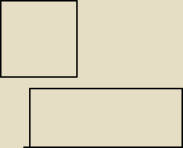
ArtuśPati: Rownolegloboki nie sa podobne na podstawie kat kat . Wytlumacze na obrazku. Oba czworakaty maja jednakowe katy a nie powiesz mi ze sa podobne.

KATALKA: czyli mam po prostu udowodnic twierdzenie o dwusiecznej?

ArtuśPati: Wystarczy ze przepiszesz to co napisalismy o 13:08

KATALKA: ja to musze zrozumiec i umiec zrobic samodzielnie