MATURA 2012 PODSTAWA. Isme: Matura tuż tuż a mnie ciągle prześladują zadania typu "wykaż" lub "udowodnij". W ogóle nie mogę sobie z nimi poradzić, ostatnio z zamkniętych miałam 22 na 25pkt a otwarte, tragedia. Zastanawiam się jak poradzić sobie z zadaniami właśnie typu "wykaż" to jest zwykłe kombinowanie czy jak? Nie potrafię sobie żadnego zadania z "wykaż" uzmysłowić i co najgorsze, zaczynam się bardzo spinać i bać.

Basiek: Ćwiczyć, ćwiczyć, ćwiczyć, ćwiczyć.... Google Ci posłużą, w razie czego pytaj

Isme: To są chyba najgorsze zadania a zorientowałam się , że na każdej maturze trafily się po dwa zadania tego typu a fajnie byłoby zdobyć te 2*2pkt bo to chyba nie jest trudne . Aczkolwiek ciągle się gubię... Najwyżej jutro zadam pytania to mi pomożecie.

Basiek: Jaaasne. Wystarczy poćwiczyć. Nie są trudne.

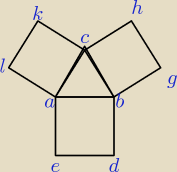
Isme: Zadanie z poprawkowej matury z sierpnia 2011r. Na bokach trójkąta równobocznego ABC (na zewnątrz tego trójkąta) zbudowano kwadraty ABDE, CBGH i ACKL. Udowodnij, że trójkąt KGE jest równoboczny. Właśnie mam problem z wytłumaczeniem tego w języku "matematycznym" Nie wiem jakbym to ujęła. Wiem, że |KG| = |GE| = |EK| Dalej myśląc widzę, że trzeba by pewnie zastosować jakąs zależność między kątami. Ale nie wiem Jak na mój mózg humanisty to cienko, ze mną. Jakieś wsparcie?

asdf: ja bym to tak zrobił, chociaż nie jestem pewien czy to dobrze: jeżeli są to kwadratY to wszystkie boki są takie same, więc: |GB| = |CB| = |BD| = |BA| = |AL| = |AC| Albo za pomocą kątów, ale to jedynie moje "przemyślenia", a ja często (nieświadomie) pisze głupoty

Isme: No tak tyle, że trzeba udowodnić, że trojkąt KGE jest równoboczny. Więc nie wiem czy trzeba jakoś zbytnio opierać się na tym ABC. yhhh..

konrad: Dla mnie to treść jest chora. Najpierw jest napisane "na trójkącie równobocznym" a potem każą wykazać, że ten trójkąt jest równoboczny O_o

konrad: aa, trójkąt kge − ślepy jestem xD

Isme: Ja na początku też zaczęłam mysleć nad trojkątem ABC ale potem mówię "zaraz chwileczke" przecież coś tu nie gra

konrad: na pewnej stronie znalazłem takie rozwiązanie: na mocy twierdzenia bok−kąt−bok trójkąty KGC, GEB i KEA są przystające, z czego wynika że boki KG, GE i EK są takie same a zatem trójkąt jest równoboczny.