 . Mam problem z pięcioma zadankami z matematyki, z ciągów, które muszę
rozwiązać na czwartek. Czułabym się bardzo wdzięczna za pomoc. Z góry dziękuję.
. Mam problem z pięcioma zadankami z matematyki, z ciągów, które muszę
rozwiązać na czwartek. Czułabym się bardzo wdzięczna za pomoc. Z góry dziękuję.  1. Dany jest ciąg an o wyrazie ogólnym an = −7+(2n:7).
a. Którym wyrazem tego ciągu jest liczba 1?
b. Ile wyrazów ujemnych ma ten ciąg?
2. Dany jest ciąg geometryczny : 4,2,1,1/2,1/4,…
a. Oblicz dziewiąty wyraz tego ciągu.
b. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
3. Oblicz sumę 7 początkowych wyrazów ciągu arytmetycznego an, jeżeli a1= −3,a12 –a9 = 15.
4. Dziadkowie w dniu narodzin wnuka zdeponowali dla niego w banku kwotę k zł na 18 lat
oprocentowaną 4 % w skali roku, z roczną kapitalizacją odsetek. Obecnie wnuczek ma 7 lat i
kwota ta wzrosła do 7895,60zł. Ile wynosił kapitał początkowy? Jaką kwotą dysponował wnuczek
w
18 urodziny?
5. Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz
długości boków i pole prostokąta. Obwód jest równy 28.
1. Dany jest ciąg an o wyrazie ogólnym an = −7+(2n:7).
a. Którym wyrazem tego ciągu jest liczba 1?
b. Ile wyrazów ujemnych ma ten ciąg?
2. Dany jest ciąg geometryczny : 4,2,1,1/2,1/4,…
a. Oblicz dziewiąty wyraz tego ciągu.
b. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
3. Oblicz sumę 7 początkowych wyrazów ciągu arytmetycznego an, jeżeli a1= −3,a12 –a9 = 15.
4. Dziadkowie w dniu narodzin wnuka zdeponowali dla niego w banku kwotę k zł na 18 lat
oprocentowaną 4 % w skali roku, z roczną kapitalizacją odsetek. Obecnie wnuczek ma 7 lat i
kwota ta wzrosła do 7895,60zł. Ile wynosił kapitał początkowy? Jaką kwotą dysponował wnuczek
w
18 urodziny?
5. Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz
długości boków i pole prostokąta. Obwód jest równy 28.



| 2n | ||
1) an = −7 + | ||
| 7 |
| 2n | ||
a) an=1, czyli rozwiąż równanie: −7+ | = 1 i podaj wynik. Sprawdzimy. | |
| 7 |
| 2n | ||
a) −7+ | = 1 /*7 | |
| 7 |
| 2n | ||
−7+ | < 0 /*7 | |
| 7 |
| 1 | ||
2n < 49 ⇒ n < 24 | ||
| 2 |
| 1 | ||
2) c.geometr.: 4,2,1, | ,... a9=? S10=? | |
| 2 |
| 2 | 1 | |||
a1=4, q= | = | |||
| 4 | 2 |
| 1 | 1 | 1 | ||||
ze wzoru na an mamy: a9=a1*qn−1 = 4*( | )8 = 4* | = | ||||
| 2 | 256 | 64 |
| 1−q10 | 1−(12)10 | 1−11024 | ||||
S10= a1* | = 4* | = 4* | = | |||
| 1−q | 1−12 | 12 |
| 1023 | 1023 | 127 | ||||
= 4* | *2 = | = 7 | ||||
| 1024 | 128 | 128 |
| a1+a7 | −3+27 | |||
S7= | *7= | *7= 12*7=84 | ||
| 2 | 2 |
 . A dałabyś radę jeszcze zad 4 i 5
. A dałabyś radę jeszcze zad 4 i 5  Jeśli nie ma Cię przypadkiem już na forum, to proszę kogoś o pomoc.
Jeśli nie ma Cię przypadkiem już na forum, to proszę kogoś o pomoc.
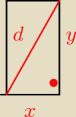 zad.5.
Przyjmij x=a1=a, b=a+r, d=a+2r
x,y,d,r>0
d2=a2+b2
2a+2b=28
Podstaw za x, y , d i rozwiąż układ równań
Niektórzy przyjmują
x=a−r, y=a, d=a+r
zad.5.
Przyjmij x=a1=a, b=a+r, d=a+2r
x,y,d,r>0
d2=a2+b2
2a+2b=28
Podstaw za x, y , d i rozwiąż układ równań
Niektórzy przyjmują
x=a−r, y=a, d=a+r
| 4 | ||
K*(1+ | )7=7895,6 | |
| 100 |
| 4 | ||
K18 = 6000*(1+ | )18 = 6000*1.0418= 6000*2,0258165 ≈ 12155 zł | |
| 100 |
