Objętość ostrosłupa
umc:
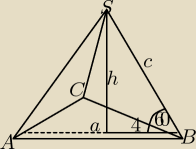
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod
kątem 60st. Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz
objętość tego ostrosłupa.
sin60 =
√32 (pierwiastek z trzech przez dwa)
√32=
4c
c=
2*4√3
c=
8√3
Czy wszystko jest jak na razie ok? bo licząc dalej coś mi nie idzie
24 kwi 19:46
umc: mógłby ktoś rzucić okiem?
24 kwi 20:02
umc: w odpowiedziach podali, że |AS'| = 8√33 a mi wyszło 8√3
gdzie jest błąd?
24 kwi 20:14
roman: no należałoby usnąć nie wymierność...
24 kwi 20:19
roman: niewymierność *
24 kwi 20:20
asdf: umc, ja nie widzę błędu
24 kwi 20:22
umc: omg racja
dzięki
24 kwi 20:24
umc: zerkniecie jeszcze na Pitagorasa? próbuję obliczyć h
h2 + a2 = (8√33)2
h2+16=643
h2=643−161
h2=643−483
h2=16
h=4
w odpowiedziach podają, że h wynosi 8
w czym tkwi problem?
24 kwi 20:35
umc: UP
24 kwi 21:14
umc: 
24 kwi 21:31
umc: 
24 kwi 21:50
umc: 
24 kwi 22:11
umc: up
25 kwi 07:30
umc: łup
25 kwi 14:36
umc: BIG UP
25 kwi 18:31