geometria Ania: W równoległoboku o obwodzie równym 144, wysokości h1 i h2 spełniają warunek ^h1_h2 = ³₅ . Oblicz długości boków tego równoległoboku.

roman: obw= 2a+2b= 144 2a+2b=144/:2 a+b=72 tylko co z tym h₁= 3 a h₂ = 5

Aga1.: a*h₁=b*h₂

roman: tak myślałem

Aga1.:

	h1		3
Ale gdy np. h1=6, a h2=10, to		=
	h2		5

Aga1.: Rozwiązywałam takie zadanie niedawno. Poszukaj.

Beti:

h1		3
	=
h2		5

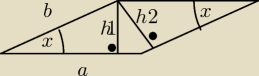
L = 2a+2b = 144/:2 a+b = 72 korzystam z funkcji tryg.:

	h1		h2
sinx =		i sinx =
	b		a

	h1		h2
więc:		=
	b		a

	h1		b
		=
	h2		a

	b		3		3
		=		−−> b =		a
	a		5		5

	3
podstawiam do obwodu: a+		a = 72
	5

	8
		a = 72
	5

a = 45

	3
b =		*45 = 27
	5

roman: tak tak ... http://www.zadania.info/7250531