Dowód Godzio: Widzę, że już jesteście, także dam zadanie (jeszcze nie to, które chciałem ).

	abc
Udowodnij wzór: R =
	4P

	1
Bez korzystania z twierdzenia cosinusów, sinusów oraz wzoru: P =		absinα
	2

Ajtek: taaaa, a świstak siedzi i zawija w sreberka .

Basiek: Godzio, mam wrażenie, że to "widzę, że już jesteście" odnosi się do mnie... Zaznaczam, że ja się nie bawię. Ale powodzenia życzę wszystkim wytrwałym

Godzio: To są zadania na myślenie Dla wszystkich

Basiek: Kobieta ma siedzieć w kuchni i nie myśleć. Zaczynam się utożsamiać.

rumpek: Czyli nic nie wolno

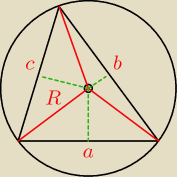
Skipper: ... da się −

rumpek: Skoro nie można korzystać z trygonometrii to kombinowałbym, podobieństwem trójkątów. Coś z tego być powinno.

Ajtek: Rysunek dużo rozjaśnił, czyli zabawa w Pitagorejczyka.

Godzio: Dorzucę drugie, niestety nie mam czasu myśleć nad dowodem, ale myślę, że wy to zrobicie, (piszę z głowy, mam nadzieję, że to prawda ) Dany jest trapez, którego suma kątów ostrych przy podstawie jest równa 90^o. Jego przekątne są

	e * f
dane, i mają długości: e i f. Pokaż, że pole takiego trapezu jest równe: P =
	2

Godzio: Wejdę wieczorem i sprawdzę wasze postępy

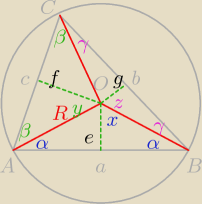
Ajtek: Takie, różne głupoty............. x, y, z − miary połowy kątów odpowiednio AOB, AOC, BOC Δ ABO, ACO i BCO są równoramienne; e, f, g ich wysokości odpowiednio. 2α+2β+2γ=180^o α+β+γ=90^o x=90−α=β+γ y=90−β=α+γ z=90−γ=α+β

	a*e		b*g		c*f		a*e+b*g+c*f
PΔABC=		+		+		=
	2		2		2		2

	a		c		b
e=		tgα, f=		tgβ, g=		tgγ
	2		2		2

	a2   b2   c2   *tgα+ tgβ+ tgγ 2   2   2		a2*tgα+b2*tgβ+c2*tgγ
zatem PΔABC=		=
	2		4

	a		b		c
R=		=		=
	2cosα		2cosβ		2cosγ

Nie mam pomysłu co dalej, nie wiem czy w dobrą stronę idę

rumpek: Przekombinowane

Ajtek: Tego się domyślam, lubię kombinować w matmie i to, jak widać, nieźle mi wychodzi . Cześć rumpek .

rumpek: Witam Witam Napisałem − najprościej zrobić podobieństwem Pamiętam jak w 2 LO męczyłem się nad wyprowadzeniem tego, jak nie miałem trygonometrii jeszcze

Ajtek: Zrobiłeś ten dwód?

rumpek: Ze 2 latka temu dlatego tutaj nie robię Zostawię tę przyjemność Wam.

Ajtek: Szczerze, to nie mam pomysłu jak to zastosować. Zerknij jeszcze, jak możesz, czy nie zrobiłem gdzieś błędu w tych wypocinach .

kylo1303: Jesli chodzi o to zadanie z trapezem to sobie napisalem 4 tw. cosinusow + kilka wzorkow na pole trojkatow z sinusem i probowalem cos wyparzyc, ale nie wyszlo za bardzo a nie chce mi sie nad tym meczyc xD

Godzio: Podbijam, bo nic nie zrobione Ajtek zdecydowanie przekombinowane, rozwiązanie ma 2 linijki max

Godzio:

Ajtek: Już jestem. Jak napisałem wcześniej, lubię kombinować, nie mylić z kombinatoryką . Na dzień dzisiejszy nic więcej nie wypocę .

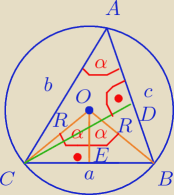
rumpek: Trójkąty prostokątne △OEB ~ △CDA (k,k,k). Oznaczę sobie wysokość trójkąta |CD| = h .

	1
P =		* h * c
	2

a   2		h
	=
R		b

	ab
Rh =		/ : R
	2

	ab
h =
	2R

	1		ab
P =		*		* c
	2		2R

	abc
P =		/ * R, R > 0
	4R

	abc
RP =		/ : P
	4

	abc
R =
	4P

c.n.u.

Godzio: O to chodziło Może za dużo zbędnego pisania, ale ok No to rumpek drugie pozostało

rumpek: Na deser jutro zrobię na razie "próbuję" pisać pracę z polskiego

Godzio: Ok, powodzenia

kylo1303: Godzio Mam pytanie. Czy jak mam rownoleglobok w ktory wpisuje romb, to: 1. boki rombu sa zawsze rownolegle do przekatnych rownolegloboku? 2. przekatne rownolegloboku zawsze dziela boki rombu na polowy?

Godzio: Z tego co pamiętam to tak, chyba kiedyś coś podobnego dowodziłem

kylo1303: Tzn ja dowiodlem ze przekatne dziela boki na polowy, tyle ze w zalozeniu mialem ze boki sa rownolegle do przekatnych. A nie wiem czy to jest uniwersalne twierdzenie. No ale dzieki.