Całka oznaczona - zadanie z treścią
olga: Mam takie zadanie i nie bardzo wiem jak do tego się zabrać?
Oblicz pole ograniczone odcinkiem osi Ox od x=0 do x=a, rzędną w punkcie x=a oraz łukiem
paraboli y=x2. Jaką część pola prostokąta o wierzchołkach (0,0), (a,0),(a,a2),(0,a2)
stanowi obliczone pole?
24 kwi 10:23
Skipper:
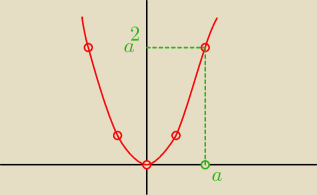
... i czego tu nie rozumiesz
?
Prosta całeczka oznaczona ...
24 kwi 11:32
olga: to będzie całka od zera do a
| | 1 | | 1 | | 1 | | 1 | |
∫ x2 dx = |
| x3 + C = |
| a3 − |
| 03 = |
| a3 |
| | 3 | | 3 | | 3 | | 3 | |
A pole prostokąta to P = a
2 x a = a
3
czyli obliczone pole to 1/3 pola prostokąta
Dobrze policzyłem?
24 kwi 11:42
Skipper:
POLAK potrafi −
24 kwi 11:45
olga: dzięki za pomoc to a mnie zgubiło.
24 kwi 11:46
Skipper: −
24 kwi 11:52