kombinuję już ze 2h i nie wiem jak rozwiązać mariusz: Dane są punkty A=(0;0) B=(3;4) oraz prosta k o równaniu y=2x+3. Wyznacz współrzędne punktu C leżącego na prostej k takiego, że pole trójkąta ABC wynosi 10.

Basiek: http://panmarek.sasiedzi.pl/ZESTAWIENIE/GEOMETRIA%20ANALITYCZNA/003%20-Zadania%20rozwiazane%20.htm Analogicznie do zadania 8−mego

mariusz: dzięki

Basiek: Nie ma problemu. Na tym forum też jest ich pełno, tego typu zadań. Wystarczy poszukać w postach Gustlika Ale to znalazłam przypadkowo, powinno pomóc. Metoda b. przydatna, warto się nauczyć

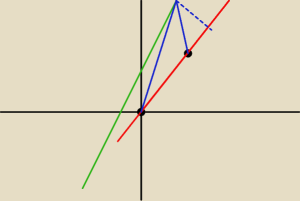
Skipper: IABI=5 aby pole wynosiło 10 ... odległość tego punktu od prostej przechodzącej przez A i B musi wynosić 4 ... i ma on spełniać równanie prostej k

Gustlik: Dane są punkty A=(0;0) B=(3;4) oraz prosta k o równaniu y=2x+3. Wyznacz współrzędne punktu C leżącego na prostej k takiego, że pole trójkąta ABC wynosi 10. A=(0;0) B=(3;4) C=(x, 2x+3) Z wektorów: AB^→=[3−0, 4−0]=[3, 4] AC^→=[x−0, 2x+3−0]=[x, 2x+3] Wyznacznik wektorów: d(AB^→, AC^→)= | 3 4 | | x 2x+3 | =3(2x+3)−4x=6x+9−4x=2x+9

	1		1
P=		|d(AB→, AC→)|=		|2x+9|
	2		2

1
	|2x+9|=10 /*2
2

|2x+9|=20 2x=−9±20 2x=11 /:2 v 2x=−29 /:2 x=5,5 v x=−14,5 y=14 v y=−26 C=(5,5; 14) v C=(−14,5; −26)

Gustlik: Basiek − rozwiąże to zad. 8 prościej, bo tam nie potrzeba żadnego układu równań:: Pole trójkąta ABC o wierzchołkach A = (– 2, – 2 ), B = (4 , 6) jest równe 21. Oblicz współrzędne wierzchołka C wiedząc, że należy on do prostej o równaniu 2x + y + 1 = 0 Najpierw przekształcę równanie prosta do postaci kierunkowej − "zrobię" z tego funkcje liniową: 2x + y + 1 = 0 y=−2x−1 Zatem: A = (–2, –2) B = (4 , 6) C=(x, −2x−1) AB^→=[4+2, 6+2]=[6, 8] AC^→=[x+2, −2x−1+2]=[x+2, −2x+1] d(AB^→, AC^→)= | 6 8 | | x+2 −2x+1| =6(−2x+1)−8(x+2)=−12x+6−8x−16=−20x−10

	1		1
Pole=		|d(AB→, AC→)|=		|−20x−10|
	2		2

1
	|−20x−10|=21 /*2
2

|−20x−10|=42 |20x+10|=42 20x=−10±42 20x=32 /:20 v 20x=−52 /:20 x=1,6 v x=−2,6 y=−2x−1 y=−4,2 v y=4,2 C=(1,6; −4,2) v C=(−2,6; 4,2)

Basiek: Tak też się staram robić. Jak najmniej zmiennych. Czasem aż przesadzam i nich z tego nie wychodzi. Ale ładnie− wektorowo

Gustlik: Ja też staram się robić na jak najmniejszej liczbie niewiadomych. Na podanej przez Ciebie stronce facet zrobił nieco naokoło, bo układem równań, i w dodatku nie przekształcał równania prostej, a wystarczyło "zrobić" postać kierunkową z równania prostej, bo wtedy rozwiązujesz po prostu ze zwykłej funkcji liniowej i jest od razu jedna niewiadoma we wzorze na pole. Ja w ogromnej większości przypadków przekształcam równanie ogólne prostej na kierunkowe, bo wtedy można rozwiązywać zadanie jak na funkcji liniowej, najczęściej maleje wtedy liczba niewiadomych, poza tym z funkcji łatwiej narysować prostą, można użyć metody "schodkowej" przy rysowaniu takiej prostej opisanej tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=41 , a więc więcej widać. Postać ogólna jest przydatna w zasadzie tylko przy obliczaniu odległości punktu od prostej, bo jest wtedy fajny wzorek, w pozostałych przypadkach najlepiej robić z funkcji liniowej. Pozdrawiam.