punkty wspólne okręgu Monika: Liczba punktów wspólnych okręgu o równaniu (x + 2)² + (y − 3)² = 4 z osiami układu współrzędnych jest: a) 0 b) 1 c) 2 d) 4 potrzebuję razem z obliczeniami, albo chociaż jakąś podpowiedź, bo siedzę nad tym cały wieczór, zapisałam tonę papieru i nic z tego nie wyszło...

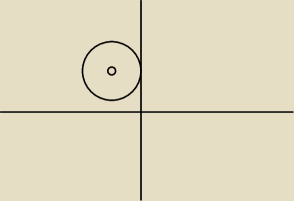
Skipper: podstaw za x=0 ... otrzymasz y=3 podstaw za y=0 otrzymasz (x+2)²=−5 ... czyli sprzeczność ... i wszystko jasne −

Mila: Moniko, narysuj ten okrąg. S=(−2,3) r=2 i wszystko zobaczysz. To jest z Aksjomatu?

krystek: Algebraicznie:Z osią OX to y=0 wstawiasz Z osią OY to x=0 wstawiasz do równania okręgu.

Monika: tak...

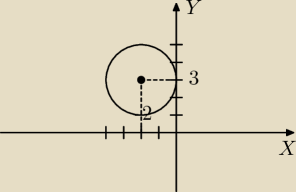
Asior: b) 1 (x−a)² + (y−b)² = r² S = (a, b) − współrzędne środka okręgu [x − (−2)]² + [y − 3]² = 2² a = −2 b = 3 r = 2 promień jest większy od odległości środka okręgu od X (nie przecina się) i równy odległości od osi Y (jeden punkt wspólny)