Całki - pole pomiędzy krzywymi kamil: Oblicz pole pomiędzy krzywymi y=|x²−1| i y=3 czy moge tutaj zrobić P=(∫(od−2 do2) 3−x²+1) − π ?

kamil:

Krzysiek: przecież pole tego kawałka paraboli którą odbijamy względem osi OX nie jest równe π ... (to nie jest funkcja sin...)

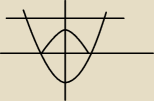
kamil: ale jakbym najpierw obliczył pole ograniczone x²−1 i y=3 i od tego odjął pole tego "koła" ?

kamil: a dobra sory to nie będzie koło

kamil: to jak w takim razie mam to obliczyc?

Krzysiek: za pomocą całki ∫₋₁¹ (1−x²) dx −pole części paraboli odbitej względem osi OX

Trivial: 1. Narysuj: http://www.wolframalpha.com/input/?i=y+%3D+|x^2-1|+%26%26+y+%3D+3 2. Ustal granice całkowania (to co nas interesuje leży pomiędzy x=−2 i x=2). 3. Oblicz całkę ∫₋₂² (3 − |x²−1|) dx. Uwaga: rozbij na 3 całki, albo zauważ, że funkcja jest parzysta i rozbij na 2 całki (rozbijamy by pozbyć się modułu).

kamil: czyli: P=(∫(od−2 do2) 3−x2+1) − (2∫(od−1do 1) (1−x2)) ?

Krzysiek: tak

Krzysiek: tak

Trivial: ∫_−2..2 (3 − |x²−1|) dx = 2 * ∫_0..2 (3 − |x²−1|) dx (funkcja jest parzysta). = 2 * ( ∫_0..1 (3 − |x²−1|)dx + ∫_1..2 (3 − |x²−1|) dx = 2 * ( ∫_0..1 (3 + x²−1)dx + ∫_1..2 (3 − x²+1) dx = 2 * ( ∫_0..1 (2 + x²)dx + ∫_1..2 (4 − x²) dx = ... (dalej już prosto).

kamil: @Trivial: Wiem, że trzeba moduł usunąć z całki. Jak to rozbić na 3 całki z tego zapisu co zaproponowałeś?

kamil: dobra dobra dobra już rozumiem dzięki Wam bardzo chłopaki

Trivial: Na końcu każdej linijki powinien być jeszcze jeden nawias ).

kamil: a możesz mi jeszcze powiedzieć jak usuwać moduł z pod całki,?

Trivial: Trzeba rozbić na odpowiednie przedziały. np. tutaj mieliśmy przedział [0, 2] (już po zauważeniu, że funkcja jest parzysta).

	⎧	x2−1, gdy x2−1 ≥ 0
|x2−1| =	⎨
	⎩	−(x2−1), gdy x2−1 < 0

czyli

	⎧	x2−1, gdy x∊[−1,1]
|x2−1| =	⎨
	⎩	−(x2−1) wszędzie indziej

Trivial: Zatem rozbijamy przedział [0, 2] na przedziały [0, 1] i [1, 2] (co chyba już widać)

Trivial: Odwrotnie napisałem. Powinno być:

	⎧	x2−1, gdy x∉[−1, 1]
|x2−1| =	⎨
	⎩	−(x2−1), gdy x∊[−1, 1]

kamil: już łapię a mam jeszcze jedno pytanie. mam obliczyć pole pod y=sinx i y=cosx dla x∊<0,2π>. jak mam znaleźć przedziały całkowania?

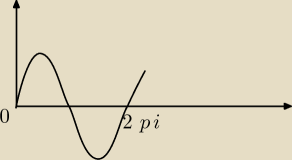
Trivial: Przedział całkowania już masz. Teraz wystarczy zauważyć, że to o co pytają wyraża się całką:

	sinx > 0 w 0..π/2
∫0..2π |sinx| dx = 4*∫0..π/2 |sinx| dx =		= 4*∫{0..π/2} sinx dx = ..

Dla cosinusa analogicznie

kamil: sory chyba troche źle sformułowałem pole ograniczone całkami y=sinx i y=cosx dla x∊<0,2π>.

kamil: *ograniczone krzywymi