Gustlik:
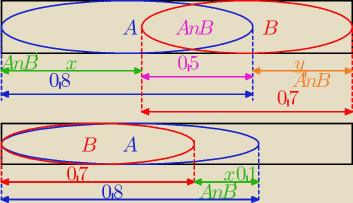
Ja to rysuje na takich diagramach jak wyżej i robię geometrycznie, wtedy widac jak na dłoni.
Z rys. 1 (od góry) mamy:
P(A∩B)=
P(A)+
P(B)−P(AUB)=0,8+0,7−1=0,5
Niech
x=P(A∩B'), a [B[y=P(A'∩B), wtedy x+y+0,5=1, stąd x+y=0,5, czyli P(A∩B`)+P(A`∩B)=0,5
Jeżeli zbiór B bedziemy "przesuwać" w lewo, to widać, że zarówno x jak i y bedą maleć, w końcu
gdy cały zbiór B stanie się podzbiorem A (rys. 2 − ten od dołu), to y==P(A'∩B)=0, a
x=P(A∩B')=0,8−0,7=0,1,0,5. Wynika stąd, że gdy B "przesunie się" w lewo, to suma
prawdopodobienstw x+y=P(A∩B`)+P(A`∩B)<0,5, bo oba prawdopodobieństwa zmaleją..
c.n.d.