Wykaż że trójkąt
Seba: Punkty D i E dzielą bok BC trójkąta ABC na trzy równe części. Wykaż, że pole trójkąta ADE jest
trzy razy mniejsze od pola trójkąta ABC
23 kwi 11:58
krystek:
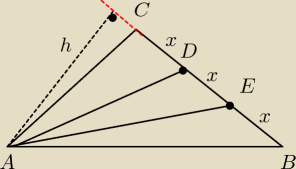
23 kwi 12:09
cywil:
Niech kąt ADB=α
Mamy zatem następujące zależności:
P
ΔADC=
12x|AD|sin(180−α)=
12|AD|xsinα
P
ΔABD=2x|AD|sinα
P
ΔABC=P
ABD+P
ACD=
123x|AD|sinα
P
ΔADE=
12x|AD|sinα
| | PΔABC | |
Czyli |
| =3 c.n.w |
| | PΔADE | |
23 kwi 15:09
