Matura próbna z Gazetą Wyborczą
rumpek: Matura Rozszerzona Gazeta Wyborcza dla wszystkich chętnych. Miłej zabawy

 Zadanie 1 (5pkt)
Zadanie 1 (5pkt)
| | 1 | | 1 | | 1 | |
Udowodnij, że jeżeli a,b,c > 0 oraz a + b + c = 1, to |
| + |
| + |
| ≥ 9. |
| | a | | b | | c | |
Zadanie 2 (5pkt)
| | 7 | |
Suma pierwszego, drugiego i trzeciego wyrazu ciągu geometrycznego (an) jest równa |
| . |
| | 4 | |
Liczby te są odpowiednio równe czwartemu, drugiemu i pierwszemu wyrazowi pewnego ciągu
arytmetycznego. Oblicz a
1, a
2, a
3.
Zadanie 3 (4pkt)
Wewnątrz trójkąta równobocznego ABC obrano taki punkt K, że jego odległość od boków AB, BC, AC
| | 1 | |
są odpowiednio równe 4 |
| , 6 i 7,5. Oblicz pole powierzchni trójkąta ABC. |
| | 2 | |
Zadanie 4 (4pkt)
Rozwiąż równanie
√3sinx * tgx − sinx −
√3 * tgx = −1 w przedziale x∊<0, 2π>.
Zadanie 5 (5pkt)
Rozwiąż nierówność |x + 2| + |x| + |x − 5| < 42.
Zadanie 6 (6pkt)
Wyznacz wszystkie wartości parametru m, dla których równanie mx
2 + (4m − 2)x + 2 − m = 0 ma co
najmniej jeden pierwiastek dodatni.
Zadanie 7 (5pkt)
W pojemniku znajduje się n kul (n≥5), z których dokładnie 5 jest białych. Wyznacz wszystkie
wartości n takie, że jeżeli będziemy losować z tego pojemnika jednocześnie dwie kule, to
| | 1 | |
prawdopodobieństwo wylosowania dwóch kul białych będzie większe od |
| . |
| | 4 | |
Zadanie 8 (5pkt)
Dla jakich wartości a i b wielomian W(x) = 2x
3 + (a − 2b)x
2 − (2a + 3b)x + 6ab dzieli się
przez reszty przez trójmian kwadratowy x
2 − 4?
Zadanie 9 (5pkt)
| | 1 | |
Rozwiąż nierówność x + log |
| (12 − 2−x) + 5 < 0. |
| | 2 | |
Zadanie 10 (6pkt)
W ostrosłupie prawidłowym czworokątnym, przekątna podstawy jest równa 8
√2. Odległość środka
symetrii podstawy od ściany bocznej jest równa
√7. Oblicz objętość i pole powierzchni
bocznej tego ostrosłupa.
*** Dodam tylko, że zadania 9 nie spotkamy na maturze, ponieważ w informatorze CKE nie ma
nierówności logarytmicznych (są tylko równania), oraz nie ma ani równań ani nierówności
wykładniczych.

23 kwi 10:08
elpe: no to lecim z tematem

23 kwi 10:15
rumpek:
Zadanie 2
a = a
4
b = a
2
c = a
1
a
n = a
1 + (n − 1)r
r = a
2 − a
1 ⇔
r = b − c
a = c + 3(b − c) ⇔
a = 3b − 2c
| ⎧ | a + b + c = 7/4 | |
| ⎨ | b2 = ac |
|
| ⎩ | a = 3b − 2c | |
2o a = 3b − 2c
3o b
2 = ac
| | 7 | | c | | 21 | | 5c | |
( |
| + |
| )2 = ( |
| − |
| ) * c |
| | 16 | | 4 | | 16 | | 4 | |
| 49 | | 7c | | c2 | | 21c | | 5c2 | |
| + |
| + |
| = |
| − |
| / * 256 |
| 256 | | 32 | | 16 | | 16 | | 4 | |
49 + 56c + 16c
2 = 336c − 320c
2
336c
2 − 280c + 49 = 0
Δ = 78400 − 65856 = 12544 ⇒
√Δ = 112
| | 280 − 112 | | 168 | | 1 | |
c1 = |
| = |
| = |
| |
| | 672 | | 672 | | 4 | |
| | 280 + 112 | | 392 | | 7 | |
c2 = |
| = |
| = |
| |
| | 672 | | 672 | | 12 | |
Będą dwa rozwiązania:
| | 7 | | 1 | | 1 | |
a = b = c = |
| ∨ a = 1, b = |
| , c = |
| |
| | 12 | | 2 | | 4 | |

Dowodu nie robię, niech każdy pomyśli

, podpowiadam tylko, że trzeba zastosować znajomości
zależności między średnimi

To zadanie 2, można jeszcze zrobić na samych a
1 i q, wtedy jest mniej obliczeń

23 kwi 10:24
rumpek:
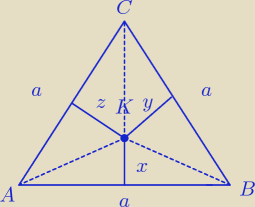 Zadanie 3
Zadanie 3
| | a√3 | | a2√3 | |
Wpierw udowodnimy, że x + y + z = |
| . Zauważmy, że PABC = |
| oraz |
| | 2 | | 4 | |
P
ABC = P
AKC + P
AKB + P
BKC.
| | 1 | | 1 | | 1 | | a2√3 | |
P = |
| * a * z + |
| * a * x + |
| * a * y = |
| |
| | 2 | | 2 | | 2 | | 4 | |
| a2√3 | | a(x + y + z) | |
| = |
| / * 4 |
| 4 | | 2 | |
a
2√3 = 2a(x + y + z)
a
√3 = 2(x + y + z)
| | a√3 | |
x + y + z = |
| = htrojkata rownobocznego |
| | 2 | |
| | 1 | | 1 | |
1) To teraz pozostanie podstawić: x = 4 |
| , y = 6, z = 7 |
| : |
| | 2 | | 2 | |
| | 9 | | 12 | | 15 | | 36 | |
x + y + z = |
| + |
| + |
| = |
| = 18 = h |
| | 2 | | 2 | | 2 | | 2 | |
| | a√3 | | a√3 | | 36√3 | |
2) h = |
| = 18 = |
| = a = |
| = 12√3 |
| | 2 | | 2 | | 3 | |
| | a2√3 | | 432√3 | |
3) P = |
| = |
| = 108√3 |
| | 4 | | 4 | |
23 kwi 10:40
rumpek:
Zadanie 4
√3sinx * tgx − sinx −
√3tgx = −1
sinx(
√3tgx − 1) −
√3tgx = − 1
sinx(
√3tgx − 1) −
√3tgx + 1 = 0
(sinx − 1)(
√3tgx − 1) = 0
1
o sinx = 1
| | π | | π | | 3π | |
x = |
| ∉ Z [ cosx ≠ 0 ⇒ x ≠ |
| ∨ x ≠ |
| ] |
| | 2 | | 2 | | 2 | |
Czyli rozwiązaniem:
23 kwi 10:45
rumpek:
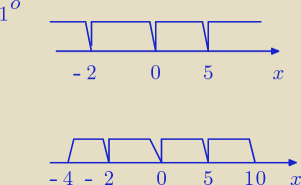 Zadanie 5
Zadanie 5
|x + 2| + |x| + 4|x − 5| < 42
Klasycznie, w przedziałach:
1
o x∊(−
∞; −2)
2
o x∊<−2; 0)
3
o x∊<0, 5)
4
o x∊<5, +
∞)
1
o x∊(−
∞; −2)
−(x + 2) − x − 4(x − 5) < 42
−x − 2 − x − 4x + 20 < 42
−6x < 24
x > −4 ⇒ x∊(−4, −2)
2
o x∊<−2; 0)
(x + 2) − x − 4(x − 5) < 42
x + 2 − x − 4x + 20 < 42
−4x < 20
x > −5 ⇒ x∊<−2; 0)
3
o x∊<0, 5)
(x + 2) + x − 4(x − 5) < 42
x + 2 + x − 4x + 20 < 42
−2x < 20
x > −10 ⇒ x∊<0, 5)
4
o x∊<5, +
∞)
(x + 2) + x + 4(x − 5) < 42
x + 2 + x + 4x − 20 < 42
6x < 60
x < 10 ⇒ x∊<5; 10)
5
o Suma rozwiązań z 1
o, 2
o, 3
o, 4
o
x∊(−4, 10)
23 kwi 10:57
miibia: rumpek mógłbyś zrobić zadanie 2 na samych a1 i q ?
23 kwi 11:20
rumpek:
Zadanie 6
mx
2 + (4m − 2)x + 2 − m = 0
1
o Sprawdzam, co się dzieje dla m = 0
−2x + 2 = 0
x = 11 ⇒ m = 0
2
o Układam warunki dla co najmniej jednego dodatniego pierwiastka, czyli wywalę przypadki gdy
oba pierwiastki są niedodatnie.
| ⎧ | Δ ≥ 0 | |
| ⎨ | x1 + x2 ≤ 0 |
|
| ⎩ | x1 * x2 ≥ 0 | |
3
o Δ = (4m − 2)
2 − 4m(2 − m) = 16m
2 − 16m + 4 − 8m + 4m
2 = 20m
2 − 24m + 4 ≥ 0
Δ
m = 576 − 320 = 256 ⇒
√Δm = 16
4
o x
1 + x
2 ≤ 0
−2m(2m − 1) ≤ 0
5
o x
1 * x
2 ≥ 0
−m(m − 2) ≥ 0
m∊<0, 2>
6
o Łączymy warunki z 4
o i 5
o
| | 1 | |
Po połączeniu otrzymamy m∊< |
| ; 2> − dla tego przedziału dwa rozwiązania są ujemne, bądź |
| | 2 | |
równe 0, zatem pozostało odczytać przeciwny przedział, dla którego będzie już co najmniej
| | 1 | |
jeden dodatni pierwiastek: m∊(−∞; |
| ) U (2, +∞). |
| | 2 | |
7
o Musimy teraz otrzymany przedział połączyć z naszą Δ ≥ 0, otrzymujemy wtedy już końcowy
| | 1 | |
wynik: m∊(−∞; |
| > U (2, +∞) |
| | 5 | |

Natomiast rozwiązanie Gazety Wyborczej mnie mocno przeraziło

zajęło im to 1/3 całej
strony

porozbijali na przypadki najdrobniejsze

23 kwi 11:27
rumpek:
Zadanie 7
| | | | n! | | (n − 1)n | |
|Ω| = Cn2 = | = |
| = |
| |
| | | 2 * (n − 2)! | | 2 | |
| | | | 5! | | 4 * 5 | |
|A| = C52 = | = |
| = |
| = 10 |
| | | 2! * 3! | | 2 | |
| 20 | | n(n − 1) | |
| > |
| |
| n(n − 1) | | 4n(n − 1) | |
| 80 | | n(n − 1) | |
| − |
| > 0 |
| 4n(n − 1) | | 4n(n − 1) | |
| −n2 + n + 80 | |
| > 0 |
| 4n(n − 1) | |
| | −1 − √321 | | 1 + √321 | |
n1 = |
| = |
| |
| | −2 | | 2 | |
| | −1 + √321 | | 1 − √321 | |
n2 = |
| = |
| |
| | −2 | | 2 | |
−4n(n − n
1)(n − n
2)(n − 1) > 0
Rozwiązujemy nierówność wielomianową i otrzymujemy przedział:
n∊(n
2, 0)U(1, n
1) nakładamy na ten przedział warunek n ≥ 5 i otrzymujemy:
n∊<5, n
2)
| | 1 + 17 | |
Pozostało obliczyć wartość n1 ≈ |
| ≈ 9 |
| | 2 | |
n∊{5,6,7,8,9} [9 dlatego, że
√321 ≈ 17,9 więc jeszcze po 9 będzie liczba, ale nie naturalna

]
23 kwi 11:41
rumpek: Dobra, trzeba sobie zrobić przerwę

23 kwi 11:41
rumpek:
Zadanie 8
W(x) = 2x
3 + (a − 2b)x
2 − (2a + 3b)x + 6ab
V(x) = x
2 − 4
Skoro ma dzielić się bez reszty czyli będą to pierwiastki tego wielomianu, zatem wystarczy
podstawić tylko x = 2 i x = −2
| ⎧ | 16 + (a − 2b)4 − (2a + 3b)2 + 6ab = 0 | |
| ⎩ | −16 + (a − 2b)4 + 2(2a + 3b) + 6ab = 0 |
|
| ⎧ | 16 + 4a − 8b − 4a − 6b + 6ab = 0 | |
| ⎩ | −16 + 4a − 8b + 4a + 6b + 6ab = 0 / * (−1) |
|
| ⎧ | 16 + 4a − 8b − 4a − 6b + 6ab = 0 | |
| ⎩ | 16 − 4a + 8b − 4a − 6b − 6ab = 0 |
|
Dodajemy teraz stronami:
32 − 8a − 12a = 0 / : 4
8 − 2a − 3b = 0
−2a = 3b − 8 / : (− 2)
Podstawiamy teraz otrzymane a pod równanie: 16 + 4a − 8b − 4a − 6b + 6ab = 0
| | 3b | | 3b | | 3b | |
16 + 4 * (4 − |
| ) − 8b − 4(4 − |
| ) − 6b + 6(4 − |
| )b = 0 |
| | 2 | | 2 | | 2 | |
16 + 16 − 6b − 8b − 16 + 6b − 6b + 24b − 9b
2 = 0
16 + 10b − 9b
2 = 0 / * (− 1)
9b
2 − 10b − 16 = 0
Δ
b = 100 + 576 = 676 ⇒
√Δb = 26
| | 10 − 26 | | 8 | | 16 | |
b1 = |
| = − |
| ∧ a1 = |
| |
| | 18 | | 9 | | 3 | |
| | 10 + 26 | |
b2 = |
| = 2 ∧ a2 = 1 |
| | 18 | |

23 kwi 12:18
rumpek:
Zadanie 9
x + log
1/2(12 − 2
−x) + 5 < 0
| | 1 | |
log1/2( |
| )x + log1/2(12 − 2−x) + 5 < 0 |
| | 2 | |
D: 12 − 2
−x > 0 ⇔ 2
−x < 12 / * log
1/2 ⇒ log
1/22
−x > log
1/212 ⇒
⇒ −xlog
1/22 > log
1/212 ⇒ x > log
1/212
| | 1 | | 1 | |
log1/2( |
| )x + log1/2(12 − 2−x) < log1/2( |
| )−5 |
| | 2 | | 2 | |
| | 1 | | 1 | |
log1/2 ( [ |
| ]x * [12 − 2−x] ) < log1/2( |
| )−5 |
| | 2 | | 2 | |
| | 1 | | 1 | |
[ |
| ]x * [12 − 2−x] > ( |
| )−5 |
| | 2 | | 2 | |
2
−x * (12 − 2
−x ) > 32
t = 2
−x, t ∊ (0, 12)
t * (12 − t) > 32
12t − t
2 > 32 / * (− 1)
t
2 − 12t + 32 < 0
Δ
t = 144 − 128 = 16 ⇒
√Δt = 4
4 < 2
−x < 8
4 < 2
−x ∧ 2
−x < 8
1
o 2
2 < 2
−x ⇒ x∊(−2, +
∞)
2
o 2
−x < 2
3 ⇒ x∊(−3, +
∞)
część wspólna :
x∊(−3, − 2)
23 kwi 12:45
amelka: utknęłam już na pierwszym

czy trzeba podstawić c = 1 − a − b ? czy jakaś inna zależność?
23 kwi 12:49
rumpek: Ogólnie na 1 zadanie, znalazłem prostszy sposób niż Wyborcza prezentuje, jak zrobię to ostatnie
to napiszę 1.
23 kwi 12:51
amelka: to w takim razie czekam z niecierpliwością

23 kwi 12:52
asdf: a masz może arkusz do podstawy

?
23 kwi 12:55
Vizer: To pierwsze bez rozwiązywania, można chyba łatwo zrobić ze związku między średnią arytmetyczna
i harmonicznej.
23 kwi 12:57
rumpek: Podstawy nie chce się przepisywać

23 kwi 12:59
asdf: nie chodzi mi o rozw. tylko o arkusz (link)
23 kwi 13:02
rumpek:
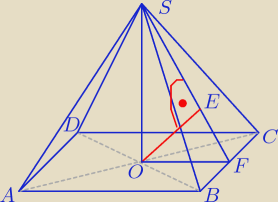 Zadanie 10
Zadanie 10
|AC| = |BD| = 8
√2
a
√2 = 8
√2 / *
√2 ⇒ a = 8, zatem odcinek |OF| = 4, |OE| =
√7. Z tw. Pitagorasa obliczmy
odległość |EF|.
|EF|
2 + |OE|
2 = |OF|
2
|EF|
2 + 7 = 16
|EF|
2 = 9, |EF| ∊ R
+, |EF| = 3
Pozostało skorzystać z podobieństwa trójkątów △OEF ~ △OES
3|SE| = 7
| | 7 | | 7 | | 9 | | 7 | | 16 | |
|SE| = |
| ⇒ |SF| = 3 + |
| = |
| + |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | | 3 | |
Pozostało obliczyć wysokość, znowu z Tw. Pitagorasa:
|SO|
2 = |SF|
2 − |OF|
2 +
| | 256 − 144 | |
|SO|2 = |
| , |SO| ∊ R+ |
| | 9 | |
| | 1 | | 256√7 | |
V = |
| * 64 * 4√7}{3} = |
| [j3] |
| | 3 | | 9 | |
P
b = 2 * a * h
| | 16 | | 256 | |
Pb = 2 * 8 * |
| = |
| [j2] |
| | 3 | | 3 | |

23 kwi 13:07
rumpek: Linku nie znajdziesz dzisiaj na internecie, pewnie Wyborcza umieści dopiero jutro w formie .pdf
23 kwi 13:08
DSGN.: odpowiedz do zadania 2 nieco krótsza
mamy ciąg geometryczny
a
1+a
2+a
3
gdzie
a
1=a
1+3r
a
2=a
1+r
a
3=a
1
z wlasnosci ciagu gemoetrycznego
(a
1+r)
2=(a
1+3r)*(a
1) → a
12+2a
1r+r
2=a
1r+3a
1r → 2a
1+r+r
2=3a
1r
→ r(r−a)=0 zatem r=0 lub r=a
| | 7 | |
wiemy ze ich suma wynosi |
| |
| | 4 | |
dla r=0
dla r=a
a
4=a+3r=1
wydaje mi sie dobrze
23 kwi 13:14
rumpek:
Zadanie 1
1 sposób:
| a + b + c | | a + b + c | | a + b + c | | b | | c | | a | |
| + |
| + |
| = 1 + |
| + |
| + |
| + 1 + |
| a | | b | | c | | a | | a | | b | |
| | b | | a | | b | | c | | a | | c | |
= 3 + ( |
| + |
| ) + ( |
| + |
| ) + ( |
| + |
| ) = (*) |
| | a | | b | | c | | b | | c | | a | |
Skorzystamy teraz z zależności: a
2 + b
2 ≥ 2ab; b
2 + c
2 ≥ 2bc; a
2 + c
2 ≥ 2ac
| | a2 + b2 | | b2 + c2 | | a2 + c2 | |
= (*) = 3 + |
| + |
| + |
| ≥ |
| | ab | | bc | | ac | |
| | 2ab | | 2bc | | 2ac | |
≥ 3 + |
| + |
| + |
| ≥ 3 + 2 + 2 + 2 ≥ 9 |
| | ab | | bc | | ac | |
c.n.u.

23 kwi 13:21
AC:
No, bardzo dobrze bo wyborcza ma błedne rozwiązanie zad 1.
mianowicie, jeśli:
i
to
nie można wnioskować,
że
23 kwi 13:28
rumpek:
Zadanie 1
2 sposób:
| 1 | | 1 | | 1 | | bc + ac + ab | |
| + |
| + |
| = |
| |
| a | | b | | c | | abc | |
1
o (a − b)
2 + (b − c)
2 + (a − c)
2 ≥ 0
2a
2 + 2b
2 + 2c
2 − 2ab − 2ac − 2bc ≥ 0
a
2 + b
2 + c
2 − ab − ac −bc ≥ 0
Dodatkowa informacja: (a + b + c)
2 = a
2 + b
2 + c
2 + 2ab + 2ac + 2bc
a
2 + b
2 + c
2 + 2ab + 2ac + 2bc ≥ 0
(a + b + c)
2 − 3ab − 3bc − 3ac ≥ 0, zatem:
| | (a + b + c)2 | | 1 | |
[ |
| ≥ ab + bc + ac ] = |
| (podstawiono a + b + c = 1) |
| | 3 | | 3 | |
2
o Średnia arytmetyczna ≥ średnia geometryczna
Podstawiając pod tezę przekształcone informacje otrzymujemy:
23 kwi 13:31
rumpek:
Sposób 2 − rozwiązanie wyborczej
Sposób 1 − moje rozwiązanie

23 kwi 13:31
rumpek:
AC a co powiesz o tym ich zadaniu 6, bo ich obliczenia skutecznie mnie przeraziły, dlatego
musiałem się chwilkę zastanowić i znalazłem krótszy sposób

23 kwi 13:35
AC:
według mnie też za bardzo szczegółowo.
A co do zad 1 to można jeszcze krócej.
Mianowicie
ŚA ≥ ŚH
| a + b+ c | | 3 | | 1 | | 1 | | 1 | |
| ≥ |
| ⇒ |
| + |
| + |
| ≥ 9 |
| 3 | | | | a | | b | | c | |
23 kwi 13:45
Ajtek:
Cześć
rumpek, zastanawiam się tylko dlaczego w zad. 6, dla m=0 x=11. Chyba literówka, mam
taką nadzieję

.
23 kwi 13:47
think: Rumpek to mnie wspuściłeś w maliny

z.5 w treści jest |x + 2| + |x| + |x − 5|
a w rozwiązaniu pojawia się 4|x − 5|

23 kwi 13:48
DSGN.: Ajtek 6 robisz zalozenie dla m≠0 bo musisz miec pierwiastki a dla m=0 masz funkcje liniową
23 kwi 13:48
rumpek:
Cześć
Ajtek. Tak literówka

x = 1 ⇒ m = 0

23 kwi 13:48
amelka: AC, tej zależności pomiędzy średnimi nie trzeba jakoś udowodnić? w ogóle to dzięki rumpek za
umieszczenie tego tutaj

23 kwi 13:49
rumpek: think a to przepraszam

nawet nie zauważyłem

ale Tak tam powinna być 4

23 kwi 13:49
Ajtek:
DSGN, dokładnie o tym wiem, mi się wynik nie zgadzał
x=11 
.
23 kwi 13:51
rumpek: Jakby jakiś admin mógł wyedytować 1 post i dostawić 4 do tej wartości bezwzględnej

23 kwi 13:51
rumpek: oj tam oj tam

za długo "jedynkę" przytrzymałem

23 kwi 13:52
AC:
Wynika to z nierówności Cauchy'ego o średnich.
23 kwi 13:52
think: luzik

dla mnie od jakiegoś czasu to najprostszy typ zadania, po prostu zaskoczylam jak
zobaczyłam różne wyniki
23 kwi 13:53
rumpek: 

23 kwi 13:53
DSGN.: no nie liczyłbym ze w maju bd taka prościzna przynajmniej stereometria i planimetria bd duzo
cięższa

to jest matura ala "operon"

23 kwi 13:55
think:
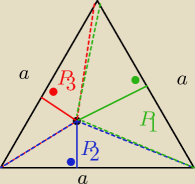
w zadaniu trzecim bym nic nie udawadniała, tylko skorzystałabym z równości pól.
P = P
1 + P
2 + P
3
ponieważ odległość punktu K od boków trójkąta to są wysokości trójkątów P
1, P
2 i P
3 to
otrzymuję:
| | 1 | |
P = |
| a(4,5 + 6 + 7,5) = 9a
|
| | 2 | |
a
2√3 − 36a = 0
a(a
√3 − 36) = 0 wtedy i tylko wtedy, gdy a = 0 lub a = 12
√3
P = 9*12
√3 = 108
√3
23 kwi 14:33
amelka: przyjemny ten arkusik

tylko pierwsze było dla mnie kłopotliwe, reszta poszła bez problemu.
obym miała podobne odczucia za dwa tygodnie

23 kwi 15:05
Gosia: dlaczego w 9 jest −do potęgi : −5 a nie do piątej?
28 kwi 20:53
Gosia: już wiem, nie trzeba

28 kwi 20:54
rafi: TEJ TO ZADANIE Z PRAWDOPODONIEŃSTWEM i kulami przecież tam można pomnożyć przez n(n−1) bo mamy
pewność żę nie będzie to zero ani wartość ujemna

!
28 kwi 21:45
Gustlik:
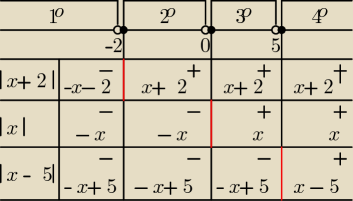
Zadanie 5 (5pkt)
Rozwiąż nierówność |x + 2| + |x| + |x − 5| < 42.
Metoda
"osi i tabelki" − najlepiej na niej widać, jak rozpisać założenia:
1
o −x−2−x−x+5<42, zał. x∊(−
∞, −2)
2
o x+2−x−x+5<42, zał. x∊<−2, 0)
3
o x+2+x−x+5<42, zał. x∊<0, 5)
4
0 x+2+x+x−5<42, zał. x∊<5, +
∞)
ad 1
o −3x<39 /:(−3)
x>−13 i x∊(−
∞, −2) ⇒ x∊(−13, −2)
ad 2
o −x<35
x>−35 i x∊<−2, 0) ⇒ x∊<−2, 0)
ad 3
o x<35 i x∊<0, 5) ⇒ x∊<0, 5)
ad 4
o 3x<45 /:3
x<15 i x∊<5, +
∞) ⇒ x∊<5, 15)
Odp: 1
o v 2
o v 3
o v 4
o ⇔ x∊(−13, 15)
29 kwi 02:41
blogther: mam pytanie do zadania 6
dlaczego takie załozenia wiem ze sa one dla dwoch ujemnych pierwiastkow ale kiedy suma dwoch
liczb ujemnych da nam 0 i kiedy iloczyn bedzie rowny 0? iloczyn bedzie 0 wtedy gdy jeden z
pierwiatkow bedzie rowny 0.....
x1 + x2 ≤ 0
x1 * x2 ≥ 0
czy te załozenie nie powinny wygladac tak
x1 + x2 < 0
x1 * x2 > 0
29 kwi 10:13
rafi: nie robimy dla dwóch ujemnych tylko dla dwóch niedodatnich

zero nie jest dodatnie
29 kwi 12:05
blogther: czyli jakie to sa liczby moze ktos podac jakis przykład?
29 kwi 12:54
def: @rumpek nie potrzebnie udowadniałeś w trzecim, leci szybko tak jak think pokazuje. Pierwsze
raczej też raczej się nie pokaże, bo nierówności o średnich nie są pokazywane w LO. Arkusz
spoko, wszystko by się zrobiło. Powodzenia na maturze!
29 kwi 14:23
rumpek: def udowodniłem, żeby ludzie którzy czytają rozwiązanie nie mieli problemów ze
zrozumieniem sposobu

29 kwi 14:24
def: @bloghter nie, założenia rumpek'a są dobre, gdy jeden z pierwiastków jest równy zero to drugi
musi być też równy 0 lub ujemny, a te rozwiązania nie są nam potrzebne.
29 kwi 14:27
29 kwi 15:24
rumpek: Są inne dane

Czytanie ze zrozumieniem
29 kwi 15:25
Gimli: POMOCY

!
Nierozumiem wogóle jak Państwo robicie zadanie 1.

Skąd wysuwacie takie zależności, z głowy ?
Np. skąd wiadomo, ze a
2 +b
2 ≥ 2ab, b
2+c
2≥2bc, a
2+c
2≥2ac
lub (a−b)
2+(b−c)
2+(a−c)
2≥0
lub (a+b+c)
2≥0 ?
Te zależności trzeba samemu zrobić, zeby rozwiazac takie zadanie, przecież ich w zadaniu nie
ma.
Jest tylko, ze a+b+c=1 i czy nie da się tego zad, rozwiazac wiedzac tylko to ?
PROSZĘ O SZYBKĄ ODPOWIEDŹ BO TEŻ PISZĘ MATURE ROZSZERZONĄ

29 kwi 15:31
rumpek: ROZWIĄZANIE GAZETY WYBORCZEJ JEST BŁĘDNE, patrz na mój 1 sposób
29 kwi 15:32
rumpek: Lub śr.gm ≥ śr. ha
29 kwi 15:32
29 kwi 15:41
Gimli: Rumpek, czy na maturze można używać tych skrótów co użyłeś :
1
o , 2
o , 3
o itd.

29 kwi 17:02
rumpek: Można, to oznaczanie określonych czynności, bardzo pomocne dla egzaminatora

29 kwi 17:03
kylo1303: W dwoch zadaniach wprowadzony zostalem w blad, mianowicie w 5 i 9. W pierwszym jak
| | 1 | |
wyczytalem nie dodales 4 (ale to jzu wiesz) a w 9 uznalem ze podstawa jest 10 a |
| laczy |
| | 2 | |
sie z nawiasem. Geometria prosta, czesc zadan meczaca przez ilosc obliczen.
29 kwi 19:07
rumpek: W 5 tak zapomniałem, natomiast 9 forum po prostu nie obsługuje podstawy ułamkowej mogłem
napisać log1/2
29 kwi 19:12
kylo1303: Wiem xD
29 kwi 19:13

 Zadanie 1 (5pkt)
Zadanie 1 (5pkt)


 Dowodu nie robię, niech każdy pomyśli
Dowodu nie robię, niech każdy pomyśli  , podpowiadam tylko, że trzeba zastosować znajomości
zależności między średnimi
, podpowiadam tylko, że trzeba zastosować znajomości
zależności między średnimi  To zadanie 2, można jeszcze zrobić na samych a1 i q, wtedy jest mniej obliczeń
To zadanie 2, można jeszcze zrobić na samych a1 i q, wtedy jest mniej obliczeń 
 Zadanie 3
Zadanie 3
 Zadanie 5
|x + 2| + |x| + 4|x − 5| < 42
Klasycznie, w przedziałach:
1o x∊(−∞; −2)
2o x∊<−2; 0)
3o x∊<0, 5)
4o x∊<5, +∞)
1o x∊(−∞; −2)
−(x + 2) − x − 4(x − 5) < 42
−x − 2 − x − 4x + 20 < 42
−6x < 24
x > −4 ⇒ x∊(−4, −2)
2o x∊<−2; 0)
(x + 2) − x − 4(x − 5) < 42
x + 2 − x − 4x + 20 < 42
−4x < 20
x > −5 ⇒ x∊<−2; 0)
3o x∊<0, 5)
(x + 2) + x − 4(x − 5) < 42
x + 2 + x − 4x + 20 < 42
−2x < 20
x > −10 ⇒ x∊<0, 5)
4o x∊<5, +∞)
(x + 2) + x + 4(x − 5) < 42
x + 2 + x + 4x − 20 < 42
6x < 60
x < 10 ⇒ x∊<5; 10)
5o Suma rozwiązań z 1o, 2o, 3o, 4o
x∊(−4, 10)
Zadanie 5
|x + 2| + |x| + 4|x − 5| < 42
Klasycznie, w przedziałach:
1o x∊(−∞; −2)
2o x∊<−2; 0)
3o x∊<0, 5)
4o x∊<5, +∞)
1o x∊(−∞; −2)
−(x + 2) − x − 4(x − 5) < 42
−x − 2 − x − 4x + 20 < 42
−6x < 24
x > −4 ⇒ x∊(−4, −2)
2o x∊<−2; 0)
(x + 2) − x − 4(x − 5) < 42
x + 2 − x − 4x + 20 < 42
−4x < 20
x > −5 ⇒ x∊<−2; 0)
3o x∊<0, 5)
(x + 2) + x − 4(x − 5) < 42
x + 2 + x − 4x + 20 < 42
−2x < 20
x > −10 ⇒ x∊<0, 5)
4o x∊<5, +∞)
(x + 2) + x + 4(x − 5) < 42
x + 2 + x + 4x − 20 < 42
6x < 60
x < 10 ⇒ x∊<5; 10)
5o Suma rozwiązań z 1o, 2o, 3o, 4o
x∊(−4, 10)
 Natomiast rozwiązanie Gazety Wyborczej mnie mocno przeraziło
Natomiast rozwiązanie Gazety Wyborczej mnie mocno przeraziło  zajęło im to 1/3 całej
strony
zajęło im to 1/3 całej
strony  porozbijali na przypadki najdrobniejsze
porozbijali na przypadki najdrobniejsze 
 ]
]


 czy trzeba podstawić c = 1 − a − b ? czy jakaś inna zależność?
czy trzeba podstawić c = 1 − a − b ? czy jakaś inna zależność?

 ?
?

 Zadanie 10
|AC| = |BD| = 8√2
a√2 = 8√2 / * √2 ⇒ a = 8, zatem odcinek |OF| = 4, |OE| = √7. Z tw. Pitagorasa obliczmy
odległość |EF|.
|EF|2 + |OE|2 = |OF|2
|EF|2 + 7 = 16
|EF|2 = 9, |EF| ∊ R+, |EF| = 3
Pozostało skorzystać z podobieństwa trójkątów △OEF ~ △OES
Zadanie 10
|AC| = |BD| = 8√2
a√2 = 8√2 / * √2 ⇒ a = 8, zatem odcinek |OF| = 4, |OE| = √7. Z tw. Pitagorasa obliczmy
odległość |EF|.
|EF|2 + |OE|2 = |OF|2
|EF|2 + 7 = 16
|EF|2 = 9, |EF| ∊ R+, |EF| = 3
Pozostało skorzystać z podobieństwa trójkątów △OEF ~ △OES




 .
.
 z.5 w treści jest |x + 2| + |x| + |x − 5|
a w rozwiązaniu pojawia się 4|x − 5|
z.5 w treści jest |x + 2| + |x| + |x − 5|
a w rozwiązaniu pojawia się 4|x − 5| 
 x = 1 ⇒ m = 0
x = 1 ⇒ m = 0 

 nawet nie zauważyłem
nawet nie zauważyłem  ale Tak tam powinna być 4
ale Tak tam powinna być 4 
 .
.

 za długo "jedynkę" przytrzymałem
za długo "jedynkę" przytrzymałem 
 dla mnie od jakiegoś czasu to najprostszy typ zadania, po prostu zaskoczylam jak
zobaczyłam różne wyniki
dla mnie od jakiegoś czasu to najprostszy typ zadania, po prostu zaskoczylam jak
zobaczyłam różne wyniki


 to jest matura ala "operon"
to jest matura ala "operon" 
 w zadaniu trzecim bym nic nie udawadniała, tylko skorzystałabym z równości pól.
P = P1 + P2 + P3
ponieważ odległość punktu K od boków trójkąta to są wysokości trójkątów P1, P2 i P3 to
otrzymuję:
w zadaniu trzecim bym nic nie udawadniała, tylko skorzystałabym z równości pól.
P = P1 + P2 + P3
ponieważ odległość punktu K od boków trójkąta to są wysokości trójkątów P1, P2 i P3 to
otrzymuję:
 tylko pierwsze było dla mnie kłopotliwe, reszta poszła bez problemu.
obym miała podobne odczucia za dwa tygodnie
tylko pierwsze było dla mnie kłopotliwe, reszta poszła bez problemu.
obym miała podobne odczucia za dwa tygodnie 

 !
!
 Zadanie 5 (5pkt)
Rozwiąż nierówność |x + 2| + |x| + |x − 5| < 42.
Metoda "osi i tabelki" − najlepiej na niej widać, jak rozpisać założenia:
1o −x−2−x−x+5<42, zał. x∊(−∞, −2)
2o x+2−x−x+5<42, zał. x∊<−2, 0)
3o x+2+x−x+5<42, zał. x∊<0, 5)
40 x+2+x+x−5<42, zał. x∊<5, +∞)
ad 1o −3x<39 /:(−3)
x>−13 i x∊(−∞, −2) ⇒ x∊(−13, −2)
ad 2o −x<35
x>−35 i x∊<−2, 0) ⇒ x∊<−2, 0)
ad 3o x<35 i x∊<0, 5) ⇒ x∊<0, 5)
ad 4o 3x<45 /:3
x<15 i x∊<5, +∞) ⇒ x∊<5, 15)
Odp: 1o v 2o v 3o v 4o ⇔ x∊(−13, 15)
Zadanie 5 (5pkt)
Rozwiąż nierówność |x + 2| + |x| + |x − 5| < 42.
Metoda "osi i tabelki" − najlepiej na niej widać, jak rozpisać założenia:
1o −x−2−x−x+5<42, zał. x∊(−∞, −2)
2o x+2−x−x+5<42, zał. x∊<−2, 0)
3o x+2+x−x+5<42, zał. x∊<0, 5)
40 x+2+x+x−5<42, zał. x∊<5, +∞)
ad 1o −3x<39 /:(−3)
x>−13 i x∊(−∞, −2) ⇒ x∊(−13, −2)
ad 2o −x<35
x>−35 i x∊<−2, 0) ⇒ x∊<−2, 0)
ad 3o x<35 i x∊<0, 5) ⇒ x∊<0, 5)
ad 4o 3x<45 /:3
x<15 i x∊<5, +∞) ⇒ x∊<5, 15)
Odp: 1o v 2o v 3o v 4o ⇔ x∊(−13, 15)
 zero nie jest dodatnie
zero nie jest dodatnie

 Czytanie ze zrozumieniem
Czytanie ze zrozumieniem
 !
Nierozumiem wogóle jak Państwo robicie zadanie 1.
!
Nierozumiem wogóle jak Państwo robicie zadanie 1.  Skąd wysuwacie takie zależności, z głowy ?
Np. skąd wiadomo, ze a2 +b2 ≥ 2ab, b2+c2≥2bc, a2+c2≥2ac
lub (a−b)2+(b−c)2+(a−c)2≥0
lub (a+b+c)2≥0 ?
Te zależności trzeba samemu zrobić, zeby rozwiazac takie zadanie, przecież ich w zadaniu nie
ma.
Jest tylko, ze a+b+c=1 i czy nie da się tego zad, rozwiazac wiedzac tylko to ?
PROSZĘ O SZYBKĄ ODPOWIEDŹ BO TEŻ PISZĘ MATURE ROZSZERZONĄ
Skąd wysuwacie takie zależności, z głowy ?
Np. skąd wiadomo, ze a2 +b2 ≥ 2ab, b2+c2≥2bc, a2+c2≥2ac
lub (a−b)2+(b−c)2+(a−c)2≥0
lub (a+b+c)2≥0 ?
Te zależności trzeba samemu zrobić, zeby rozwiazac takie zadanie, przecież ich w zadaniu nie
ma.
Jest tylko, ze a+b+c=1 i czy nie da się tego zad, rozwiazac wiedzac tylko to ?
PROSZĘ O SZYBKĄ ODPOWIEDŹ BO TEŻ PISZĘ MATURE ROZSZERZONĄ 

