tw. cosinusów pszczółka maja: Pomocy! Jak wyznaczyć długości środkowych trójkąta o bokach a,b i c?

radek: jezeli chcesz zastosowac tw cosinusow to bierzesz pierwszy bok, polowe drugiego boku, oraz cosinus kata pomiedzy nimi i poprostu dajesz do wzoru

pszczółka maja: ale jeśli nie znam kąta..?

radek: jak znasz dlugosc trzech bokow to z twierdzenia cosinusow liczysz kat

radek: znaczy jego cosinus bo a²= b² + c² − 2bc*cosα a potrzebujesz cos tylko podstawiasz dlugosci bokow

radek: czyli wpierw liczysz kat z twierdzienia cosinusow a potem, srodkawa rowniez z twierdzenia cosinusow tylko zmieniasz dane we wzorze

pszczółka maja: ale nie mam danych żadnych. Zadanie brzmi: Wyznacz śrokowe w trójkącie o bokach a,b i c. Tyle

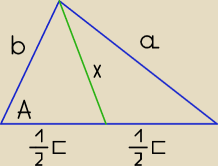
Bogdan: Wyprowadzę wzór na środkową x wg przepisu radka, bo to jest dobry sposób, w podobny sposób wyprowadza się wzory na środkowe y, z. A − miara kąta między bokami b oraz c. Korzystamy dwukrotnie z wzoru kosinusów:

	−a2 + b2 + c2
a2 = b2 + c2 − 2bc cosA => cosA =
	2bc

	1		1
x2 = b2 +		c2 − 2b*		c cosA =
	4		2

	1		−a2 + b2 + c2
= b2 +		c2 − bc *		=
	4		2bc

	1		1		1		1		2a2 + 2b2 − c2
= b2 +		c2 +		a2 −		b2 −		c2 =
	4		2		2		2		4

	1
x =		√2a2 + 2b2 − c2
	2