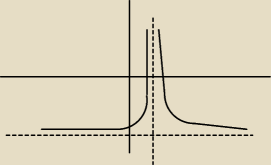
znajdź m ADm: Siemanko Narysuj wykres funkcji określonej wzorem f(x) = |¹_x−1| − 4 . na podstawie jej wykresu wyznacz zbiór wszystkich wartości parametru m, dla których równanie f(x) = log₂. I tak, narysowałem wykres, może nie jest pierwszej młodości ale ogarnąć go można. asymptoty znajdują x,y znajdują się kolejno 1, −4. Moje pytanie dotyczy druggiej części zadania. Co należy zrobić. Wiem że m musi być większe od 0. Ale to nie jest jedyny warunek . Jaki jest drugi warunek i dlaczego on występuje? dziękuję z góry za odpowiedź .

Aga1.: Pierwsza część dobrze zrobiona, a druga nie zapisana poprawnie, więc nikt nie może Ci pomóc.

ADm: f(x)= log₂m sorry xd

Gdańszczanin: Czegoś tam brakuje np. "dla których równanie f(x)=log₂m ma dwa rozwiązania.

ADm: ...nie ma rozwiązań. Kurde sory, mało spałem w nocy. jak się liczy takie równania?

Gdańszczanin: Patrzysz na wykres, i patrzysz jakich wartości funkcja nie osiąga (−nieskończoność;−4>. Czyli brak rozwiązań dla f(x)=k kiedy 4≥k 4≥log₂m log₂16≥log₂m 16≥m (nie zmieniamy znaku bo podstawa logarytmu jest większa od 1)

ADm: ok. dzięki wielkie.