oblicz cosinus kąta pepa: Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi. Wyszedł mi cos=^√15₄ , mógłby ktoś to sprawdzić?

pepa: ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

pepa: ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

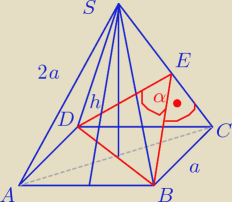
rumpek: |BD| = a√2 |BE| = |DE| = h₁ = wysokość trójkąta równoramiennego BCS, obliczymy ją w następujący sposób:

	a2
4a2 =		+ h2
	4

	a2
h2 = 4a2 −
	4

	16a2 − a2
h2 =
	4

	15a2
h2 =		, h∊R+
	4

	√15a
h =
	2

	1
P =		a * h
	2

	1
P =		* 2a * h1
	2

1		1
	* a * h =		* 2a * h1 / * 2
2		2

a * h = 2a * h₁

	√15a
a *		= 2a * h1
	2

	a√15
h1 =
	4

2^o Zastosujmy tw. cosinusów: (a√2)² = h₁² + h₁² − 2h₁ * h₁ * cosα

	15a2		15a2		15a2
2a2 =		+		− 2 *		* cosα
	16		16		16

	30a2		15a2
2a2 =		−		cosα / * 16
	16		8

32a² = 30a² − 30a²cosα 2a² = −30a²cosα / : (−30a), bo a > 0

	1
cosα = −
	15