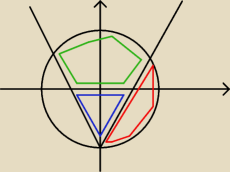
Wyliczanie fragmentu koła w układzie współrzędnym Max__: Oblicz pole części koła ograniczonej prostą o równaniu y =√3x − 2√3, obrazem tej prostej w symetrii względem osi OY i tą częścią okręgu x²+y²= 12, która leży ponad osia OX Kolorowe na rysunku służą do wskazania odpowiednich figur. Poniżej są moje wyliczenia do tego zadania. Byłbym bardzo wdzięczny jakby ktoś sprawdził gdzie popełniłem,błąd albo chociaż sam zrobił to zadanie i napisał czy ma taki sam wynik jak w książce. Z góry dziękuje Dzisiaj zabrałem się za takie zadanie. Chciałem je zrobić następująco: r=2√3 więc Pole koła = 12π Wiem że proste przecinają się z osią OX w punktach −2 i 2 więc podstawa niebieskiego trójkąta ma długość 4 a wysokość 2√3. Zatem jego pole jest równe 4√3. Układ równań jednej prostej i koła dał mi współrzędne przecięcia się A = (0,2√3) i B = (3 , √3) Obliczyłem długość odcinka |AB| = 6 Przyjmując że S to środek okręgu to trójkąt SAB jest równoramienny. Z twierdzenia cosów wyszło mi że kąt α przy wierzchołku S jest równy 120 stopni. Tak więc pole trójkąta jest równe 3√3 Pole części koła która zawiera ten trójkąt jest równa 4π Pole czerwonej figury jest więc równe 4π − 3√3 Pole figury zaznaczonej na zielone jest więc równe całość koła odjąć dwa razy czerwone i odjąć niebieskie 16π − 8π + 6√3 − 4√3 = 8π + 2√3 − Taka wg mnie jest odpowiedz ale niestety w książce pisze, że poprawna odpowiedz to 8π + 6√3 − Nie mam pojęcia dlaczego proszę o pomoc.