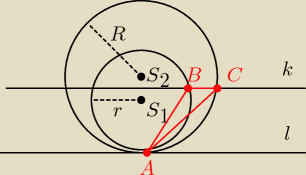
Okregi ................: MEGA TRUDNE ZADANIE (jak dla mnie) Okręgi O1 o srodku S1 i promieniu r i O2 o srodku S2 i promieniu R są styczne do prostej l w punkcie a. Prosta k jest równoległa do prostej l i przecina okregi O1 i O2 odpowiednio w punktach Bi C. Wyznacz promień x okręgu opisanego na trójkącie ABC w zależności od promienia r i R.

................: pomóżcie

................: POMOCY

................: jak ktoś umie to niech pomoże

................: ?

Alkain: Dobra zacznijmy od tego co mamy wyznaczyć. Tzn. promień okręgu opisanego na trójkącie ABC. Wzór na promień okręgu opisane na trójkącie

	abc
X=
	4P

Czyli musimy wyznaczyć boki a,b,c i P tego trójkąta w zależności od promieni. Jakie zadanie... xD Odcinek |AC| niech to będzie nasze a |AC|²=R²+R²−2R²cosα AB− nasze b |AB|²=r²+r²−2r²cosβ Nie mam pomysłu jak policzyć BC Do pola potrzeba jakiś bok i wysokość. Na wysokość też nie mam pomysłu. Ciekawe zadanie...

Aga1.: R można wyznaczyć z twierdzenia sinusów. Myślałam nad tym zadaniem,chyba trzeba zauważyć własności kątów ( i tu utknęłam). Wtedy IBCI liczy się z pól Na razie zniechęciłam się,ale myślę, że powrócę do tego zadania.

MQ: Wydaje mi się, że będzie to też zależeć od odległości k od l, która nie została tu podana.

Alkain: MQ te zadanie chyba tak wygląda znalazłem podobne z jakiegoś konkursu http://students.mimuw.edu.pl/~am234204/10lat.pdf str. 16 zadanie 10. Ale i tak dalej nie mam pomysłu jak to policzyć :<

MQ: Policzyłem to analitycznie (środek ustawiłem w p. A) i......... o dziwo wyszło mi x=√Rr Jeśli się oczywiście gdzieś nie walnąłem

................: Możecie to jakoś wytłumaczyć bardzo proszę

................: ponawiam

MQ: Jak już napisałem wcześniej, zrobiłem to analitycznie. Mogę to więc opisać w skrócie, bo byłoby dużo wypisywania. Środek układu (0,0) umieściłem w p. A. Oś OY przechodzi przez S₁(0,r) i S₂(0,R).

MQ: przycisnąłęm nie to co trzeba −− dalszy ciąg za chwilę.

MQ: Prosta k jest w odległości k od OX stąd obliczyłem: x_B=√k(2r−k) i x_C=√k(2R−k) Potem obliczyłem równania dwusiecznych:

	xB
Dwusieczna AB: y=−		*x+r
	k

	xC
Dwusieczna AC: y=−		*x+R
	k

Stąd wsp. środka okręgu opisanego: x_S=(x_B+x_C)/2 y_S=k−U{x_B*x_C}/k Z trójkąta równoramiennego BCS łatwo już znaleźć, że x=√Rr

................: Dziękuje bardzo