Stozek Ufo: W stozek o wysokosci 10 wpisano kule o promieniu 4. Oblicz pole powierzchni całkowitej stozka.

Eta: P_c=200 π

Klops: Eta, a jak to obliczyłaś ?

Eta: Zaraz narysuję

Klops: okej chciałam pomóc koledze, a tak się głowie i wymyślić nie mogę, przy okazji ćwiczę sobie do matury, przyda się

picia: pamietam ze na ustnej mialem kule w walcu czy stozku i prawie zadnych.i do wszystkiego doszedlem ze wzoru pitagorasa,tylko nawynajdywalem tych trojkatow ze jak przy stoliku mowilem to az mi bylo glupiociekawe czy tu jest podobnie.

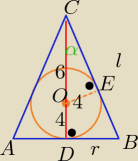
Eta: r −−− dł. promienia podstawy stożka ΔBDC ~ ΔOEC z cechy (kkk)

r		4		2
	=		⇒ r=		l
l		6		3

	4
z tw. Pitagorasa w Δ DBC l2= 100+		l2 ⇒ l=....... = 6√5
	9

r=..... P_c=...... dokończ..........

Klops: oby nie o.O

picia: i od tej pory twierdzenie pitagorasa jest moim ulubionym.

picia: oo i niesmiertelny moj ulubiony wzorhaha

Skipper:

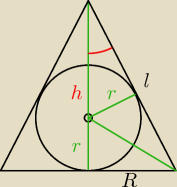
r
	=sinα ... ⇒ sinα=2/3 cosα=? ... tgα=?
10−r

policzysz R i tworzącą ... i dalej już z górki ...−