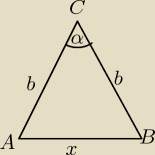
W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC|=|BC|=b oraz I<ACBI=α. Z wierzchołka B
przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok AC w
punkcie D. Oblicz promień okręgu wpisanego w trójkąt.
Proszę o dokończenie, nie wiem co z tym dalej zrobić.
x2=2b2−2b2cosα=2b2(1−cosα)
x=√2b2(1−cosα)=b√2(1−cosα)
| abc | ||
P=pr i P= | ||
| 4R |
| x | ||
2R= | ||
| sinα |
| b√2(1−cosα) | ||
R= | ||
| 2sinα |
| abc | ||
pr= | ||
| 4R |
| b+b+2b2(1−cosα) | b2*2b2(1−cosα) | |||||||||
r* | = | |||||||||
| 2 |
|
| sinα | ||
r= | ||
| √2(1−cosα) |