| P(A∩B) | ||
P(A/B) = | ||
| P(A) |
| n*(n−1) + (10−n)*n | ||
P(A) = | ||
| 10*9 |
| (10−n)*n | ||
P(A∩B) = | ||
| 10*9 |
| (10−n)*n | 10−n | 2 | ||||
P(A/B) = | = | = | ||||
| n*(n−1+10−n) | 9 | 3 |
 W urnie znajdują się kule białe i czarne, razem jest ich 10. Losujemy bez zwracania dwie kule.
Prawdopodobieństwo wylosowania za drugim razem kuli białej, pod warunkiem że za pierwszym
razem wylosowaliśmy kulę czarną, jest równe 2/3. Ile kul białych jest w urnie?
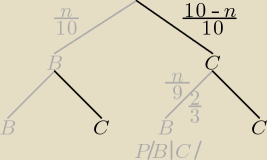
I tu się właśnie przydaje krzakoterapia, do prawdopodobieństwa warunkowego i całkowitego, bo
"odnogi" drzewka to właśnie prawdopodobieństwa warunkowe:
Kul białych mamy n, czarnych 10−n
W urnie znajdują się kule białe i czarne, razem jest ich 10. Losujemy bez zwracania dwie kule.
Prawdopodobieństwo wylosowania za drugim razem kuli białej, pod warunkiem że za pierwszym
razem wylosowaliśmy kulę czarną, jest równe 2/3. Ile kul białych jest w urnie?
I tu się właśnie przydaje krzakoterapia, do prawdopodobieństwa warunkowego i całkowitego, bo
"odnogi" drzewka to właśnie prawdopodobieństwa warunkowe:
Kul białych mamy n, czarnych 10−n
| n | 2 | ||
= | |||
| 9 | 3 |