F.kwadratowa.
Żabcia: Proszę o sprawdzenie



Zadanie: Dana jest funkcja kwadratowa y=−x
2−x+
34.
a) Oblicz współrzędne wierzchołka paraboli, która jest wykresem tej funkcji.
Odp: y=−x
2−x+
34 −postać ogólna
y=a(x−p)
2 +q −postać kanoniczna
a=−1 b=−1 c=
34
Δ=−1
2−4*(−1)*
34
Δ=1+
124=1+3=4
p=
−b2a
p=
12*(−1)=
1−2=−
12
q=
−Δ4a
q=
−44*(−1)=
−4−4=1
y=a(x−p)
2+q
y=−1(x+
12)
2+1 −p.kanoniczna
W(−
12, 1) −współrzędne wierzchołka paraboli.
20 kwi 10:10
Bogdan:
Dobrze, z tym, że:
1. Postać kanoniczna: y = (x + 12)2 + 1
zazwyczaj nie piszemy jedynki przed nawiasem.
2. Współrzędne wierzchołka oznaczamy xw, yw, a nie p, q.
Oznaczenia p, q to współrzędne wektora przesunięcia paraboli z punktu O(0, 0)
do punktu W(xw, yw).
20 kwi 10:40
Żabcia: Ok. Dziękuje za poprawienie

Z przyzwyczajenia pisze p i q bo tak mnie uczyli w
gimnazjum i teraz w liceum też tak piszą.

20 kwi 10:44
Żabcia: Do tego samego zadania.
b) Oblicz miejsca zerowe tej funkcji.
y=−x2−x+34
a=−1 b=−1 c=34
Δ=4
x1=12
x2=−112
Miejsca zerowe to:
x=12 i x=−112
20 kwi 10:49
Bogdan:
Współrzędną y
w wierzchołka można obliczyć bez Δ.
Sposób 1.
| | 1 | |
Wyznaczamy xw, w tym zadaniu xw = − |
| |
| | 2 | |
| | 1 | | 1 | | 1 | | 3 | | 1 | | 2 | | 3 | |
yw = f(− |
| )= −(− |
| )2 − (− |
| ) + |
| =− |
| + |
| + |
| = 1 |
| | 2 | | 2 | | 2 | | 4 | | 4 | | 4 | | 4 | |
Sposób 2.
y
w = c − a*(x
w)
2
| | 3 | | 1 | | 3 | | 1 | |
yw = |
| + 1*(− |
| )2 = |
| + |
| = 1 |
| | 4 | | 2 | | 4 | | 4 | |
20 kwi 10:51
Bogdan:
Miejsca zerowe − dobrze
20 kwi 10:52
Żabcia: O tego nie wiedziałam

20 kwi 10:53
Żabcia:
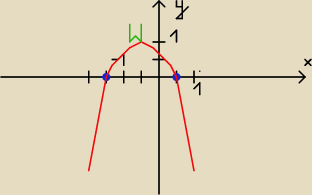
Dalsza część zadania:
c) Narysuj wykres tej funkcji.
Więc mam:
W(−
12, 1)
miejsca zerowe:
12 i −1
12
hmm rysować nie potrafie także jest troszke niedokladnie ale czy dobrze?
20 kwi 11:03
Bogdan:
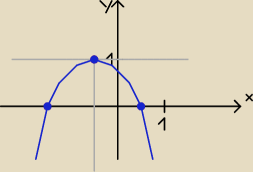
Dobrze. Warto zaznaczać oś paraboli, a także prostą przechodząca
przez wierzchołek i równoległą do osi x.
20 kwi 11:38
Żabcia: Oki dziękuje

d) Zbadaj monotoniczność tej funkcji.
Odp:
funkcja rośnie dla x E(−∞, −
12>
funkcja maleje dla x E<−
12, ∞)
20 kwi 11:42
Żabcia: Zadanie: Rozwiąż nierównośi kwadratowe:
a) −3x
2>48
b)
23x
2+
43x≤0
c) −3x
2+15x−12<0
Jak mam to wykonać?Proszę o jakąś podpowiedź jak się do tego zabrać

20 kwi 12:17
Bogdan:
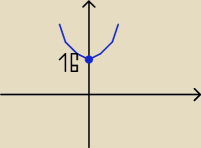
Monotoniczność dobrze.
Nierówności:
a) 3x
2 + 48 < 0 => x
2 + 16 < 0 x należy do zbioru pustego.
Widać na rysunku, że parabola y = x
2 + 16 jest położona nad osią x, czyli
dla wszystkich wartości x funkcja f(x) jest dodatnia, a nie ujemna.
20 kwi 12:34
Bogdan:
b) W nierównościach typu ax
2 + bx ≤ 0 lub < 0 lub > 0 lub ≥ 0
wyłączamy ax przed nawias.
+ + + + + +
| | 6 | |
−−−−−−−−− (− |
| ) −−−−−−−−−− (0) −−−−−−−−−−> |
| | 5 | |
− − −
20 kwi 12:42
Bogdan:
c) Warto sprawdzić, czy można uprościć nierówność.
−3x2 + 15x − 12 < 0 /:(−3)
x2 − 5x + 4 > 0
wyznacz x1, x2, naszkicuj na osi parabolę i odczytaj przedział spełniający
nierówność
20 kwi 12:47
Żabcia: Zadanie: Drut o długości 120 cm chcemy wygiąć w prostokątną ramkę. Oblicz, jakie wymiary
powinna mieć ta ramka, aby prostokąt, który ogranicza, miał największe pole.
Jak to wykonać?
20 kwi 15:06
Bogdan:
a, b − długości boków prostokątnej ramki.
2a + 2b = 120 => b = 60 − a
Pole P = ab => P = a(60 − a)
Otrzymaliśmy funkcję kwadratową P(a) = −a2 + 60a, która osiąga maksimum
dla a = 30 (odcięta wierzchołka paraboli),
b = 30.
20 kwi 15:16
Żabcia: A jest jakiś prościejszy sposób na rozwiązanie tego zadania?
20 kwi 16:06
tim: Metoda prób i błędów?
20 kwi 16:07
Żabcia: Hmm nie bardzo rozumiem...
20 kwi 16:08
Bogdan:
A co Żabciu widzisz tu nieprostego?
To już jest przecież proste.
20 kwi 16:08
Żabcia: Nie rozumiem skąd się co bierze...
20 kwi 16:12
Bogdan:
Otrzymalismy funkcję P(a) = −a2 + 60a, której wykresem jest parabola skierowana
ramionami w dół, a więc parabola ta posiada maksimum w wierzchołku.
20 kwi 16:12
Żabcia: Aha nio to rozumiem.
20 kwi 16:14
Bogdan:

Obwód prostokąta 2a + 2b = 120 => a + b = 60 => b = 60 − a
Pole prostokąta P = ab => P = a * (60 − a) => P = −a
2 + 60a
Jak widać, pole P zależy od a, mamy więc określoną funkcję P(a) = −a
2 + 60a,
jest to funkcja kwadratowa, którą zajmujesz się dzisiaj.
We wzorze tej funkcji występuje zmienna a (nie zawsze przecież bedzie x, to jest
tylko kwestia oznaczeń).
20 kwi 16:21
sadfsdf: βsdsdfdwwd
20 kwi 16:24
Żabcia: oki

Dziękuje

20 kwi 16:31


 Zadanie: Dana jest funkcja kwadratowa y=−x2−x+34.
a) Oblicz współrzędne wierzchołka paraboli, która jest wykresem tej funkcji.
Odp: y=−x2−x+34 −postać ogólna
y=a(x−p)2 +q −postać kanoniczna
a=−1 b=−1 c=34
Δ=−12−4*(−1)*34
Δ=1+124=1+3=4
p=−b2a
p=12*(−1)=1−2=−12
q=−Δ4a
q=−44*(−1)=−4−4=1
y=a(x−p)2+q
y=−1(x+12)2+1 −p.kanoniczna
W(−12, 1) −współrzędne wierzchołka paraboli.
Zadanie: Dana jest funkcja kwadratowa y=−x2−x+34.
a) Oblicz współrzędne wierzchołka paraboli, która jest wykresem tej funkcji.
Odp: y=−x2−x+34 −postać ogólna
y=a(x−p)2 +q −postać kanoniczna
a=−1 b=−1 c=34
Δ=−12−4*(−1)*34
Δ=1+124=1+3=4
p=−b2a
p=12*(−1)=1−2=−12
q=−Δ4a
q=−44*(−1)=−4−4=1
y=a(x−p)2+q
y=−1(x+12)2+1 −p.kanoniczna
W(−12, 1) −współrzędne wierzchołka paraboli.
 Z przyzwyczajenia pisze p i q bo tak mnie uczyli w
gimnazjum i teraz w liceum też tak piszą.
Z przyzwyczajenia pisze p i q bo tak mnie uczyli w
gimnazjum i teraz w liceum też tak piszą.

 Dalsza część zadania:
c) Narysuj wykres tej funkcji.
Więc mam:
W(−12, 1)
miejsca zerowe: 12 i −112
hmm rysować nie potrafie także jest troszke niedokladnie ale czy dobrze?
Dalsza część zadania:
c) Narysuj wykres tej funkcji.
Więc mam:
W(−12, 1)
miejsca zerowe: 12 i −112
hmm rysować nie potrafie także jest troszke niedokladnie ale czy dobrze?
 Dobrze. Warto zaznaczać oś paraboli, a także prostą przechodząca
przez wierzchołek i równoległą do osi x.
Dobrze. Warto zaznaczać oś paraboli, a także prostą przechodząca
przez wierzchołek i równoległą do osi x.
 d) Zbadaj monotoniczność tej funkcji.
Odp:
funkcja rośnie dla x E(−∞, −12>
funkcja maleje dla x E<−12, ∞)
d) Zbadaj monotoniczność tej funkcji.
Odp:
funkcja rośnie dla x E(−∞, −12>
funkcja maleje dla x E<−12, ∞)

 Monotoniczność dobrze.
Nierówności:
a) 3x2 + 48 < 0 => x2 + 16 < 0 x należy do zbioru pustego.
Widać na rysunku, że parabola y = x2 + 16 jest położona nad osią x, czyli
dla wszystkich wartości x funkcja f(x) jest dodatnia, a nie ujemna.
Monotoniczność dobrze.
Nierówności:
a) 3x2 + 48 < 0 => x2 + 16 < 0 x należy do zbioru pustego.
Widać na rysunku, że parabola y = x2 + 16 jest położona nad osią x, czyli
dla wszystkich wartości x funkcja f(x) jest dodatnia, a nie ujemna.
 Obwód prostokąta 2a + 2b = 120 => a + b = 60 => b = 60 − a
Pole prostokąta P = ab => P = a * (60 − a) => P = −a2 + 60a
Jak widać, pole P zależy od a, mamy więc określoną funkcję P(a) = −a2 + 60a,
jest to funkcja kwadratowa, którą zajmujesz się dzisiaj.
We wzorze tej funkcji występuje zmienna a (nie zawsze przecież bedzie x, to jest
tylko kwestia oznaczeń).
Obwód prostokąta 2a + 2b = 120 => a + b = 60 => b = 60 − a
Pole prostokąta P = ab => P = a * (60 − a) => P = −a2 + 60a
Jak widać, pole P zależy od a, mamy więc określoną funkcję P(a) = −a2 + 60a,
jest to funkcja kwadratowa, którą zajmujesz się dzisiaj.
We wzorze tej funkcji występuje zmienna a (nie zawsze przecież bedzie x, to jest
tylko kwestia oznaczeń).
 Dziękuje
Dziękuje