zadanie mikołaj: Parabola y²=2x dzieli koło x²+y²≤8 na dwie figury. Oblicz stosunek pól tych figur. Nie wiem jak to zrobić.

	3π+2
Powinno wyjść
	9π−2

mikołaj: mógłby ktoś mi pomóc, bardzo proszę

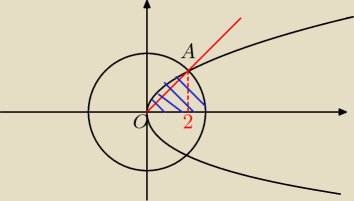
Basia: punkty wspólne okręgu i paraboli: x² + 2x = 8 x² + 2x − 8 = 0 Δ=4−4*1*(−8) = 36 √Δ = 6

	−2−6
x1 =		= −4
	2

	−2+6
x2 =		= 2
	2

x₁ = −4 nie spełnia warunków zadania bo byłoby y² = 2(−4)= − 8 sprzeczność x = 2 ⇒ y² = 4 ⇒ y=−2 lub y=2 A(2,2) B(2,−2) piszę równanie prostej OA y = ax 2 = a*2 a=1 pr.OA y=x P₀ = pole obszaru niebieskiego = ¹₈*pole koła + ₀∫² [ √2x − x] dx =

π*8
	+0∫2√2*x12 dx − 0∫2 x dx =
8

	x3/2		x2
π + √2*		0|2 −		0|2 =
	32		2

	2√2		1
π +		*[ 23/2 − 03/2] −		*[22−02] =
	3		2

	2√2		8		3π + 8 − 6		3π+2
π +		*√8 − 2 = π +		− 2 =		=
	3		3		3		3

P₁ = 2*P₀

	2(3π+2)
P1 =
	3

P₂ = pole koła − P₁

	6π+4		24π − 6π − 4		18π−4		2(9π−2
P2 = 8π −		=		=		=
	3		3		3		3

P1		3π+2
	=
P2		9π−2

mikołaj: dziękuję bardzo Basiu

mikołaj: Jeszcze mam takie zadanie, którego nie potrafię zrobić. Byłbym bardzo wdzięczny gdyby ktoś mi pomógł Zad.Oblicz pola obszaru ograniczonego krzywymi y=x²; y=2^x; x=2; x=4

Krzysiek: patrzysz która funkcja w przedziale (2,4) jest nad drugą z rysunku widać, że x² jest nad więc masz do policzenia całkę: ∫₂⁴ x² −2^x dx

mikołaj: mógłbyś mi pomóc rozwiązać tą właśnie całkę bo nie wiem jak ją rozwiązać

Krzysiek: rozbij na dwie całki i skorzystaj z podstawowych wzorów jak się liczy takie całki

mikołaj:

	1		24−22
czyli		[43−23]−		?
	3		ln2

Krzysiek: tak

mikołaj: A jaka będzie całka z tych dwóch wykresów parabol? y=x²−x−6 y=−x²−x+2

Krzysiek: http://www.wolframalpha.com/input/?i=%7By%3Dx%5E2+-x-6+%2C+y%3D-x%5E2+-x%2B2+%7D masz obszar narysowany, spróbuj Sam napisać jak ma wyglądać ta całka

mikołaj:

	1		−1
czyli granice tej całki będą od		do
	2		2

∫−x²−x+2−x²−x−6dx

Krzysiek: przecież te wykresy przecinają się w punktach −2 i 2... więc mamy: ∫₋₂² (−x² −x+2)−(x² −x−6) dx