wartość bezględna i równanie kwadratowe bum : Ix²−1I= −IxI+1

M:

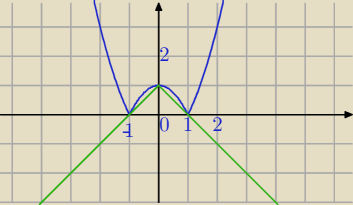Mila: Graficznie:

Bo_ra: x²−1≥0 dla x∊(−∞, −1]U[1,∞) wtedy |x²−1|=x²−1 x²−1<0 dla (−1,1) wtedy |x²−1|=−(x²−1)=1−x² |x|=x dla x≥0 x∊[0,∞) |x|=−x dla x<0 x∊(−∞,0) 1)przedział x∊(−∞,−1] |x²−1|=x²−1 |x|=−x x²−1=−(−x)+1 x²−1−x−1=0 x²−x−2=(x+1)(x−2)=0 x=−1 ∊(−∞,−1] x=2 nie należy 2) przedział x∊(−1,0] |x²−1|=1−x² |x|=−x 1−x²=x+1 −x²−x=0 x²+x=0 x(x+1)=0 x=0 x=−1 x=0 ∊(−1,0] x=−1∉(−1,0] 3)przedzial x∊(0,1] |x²−1|=1−x² |x|=x 1−x²=−x+1 −x²+x=0 x²−x=0 x(x−1)=0 x=0 ∉(,1] x=1 ∊(0,1] 4 przedział x∊(1,∞) |x²−1|=x²−1 |x|=x x²−1=−x+1 x²+x−2=(x−1)(x+2)=0 x=1∉(1,∞) x=−2 ∉(1,∞) Odp. x=−1 , x=0 , x=1