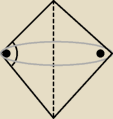
Trójkąt prostokątny o przyprostokątnych długości 15 cm i 20 cm obraca się wokół
przeciwprostokątnej. Oblicz V i pc powstałej bryły. Tak wygląda ta figura? (rysunek)
Podzieliłem sobie tą figurę na 2 stożki:
r1 = 12, h1 = 9 → V1 = 432
oraz
r2 = 12 h = 16 → V2 = 768
Vtego czegoś 
= 1200 cm3
Jest jakiś inny sposób na policzenie "tego czegoś"
Wystarczy mi po krótce przedstawienie sposobu.
Z góry dziękuję.
wyszło
| r2 | |
*π(h1 + h2) | |
| 3 |
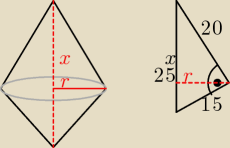Można łatwo wykazać, dodając objętości stożków, że objętość bryły powstałej ze sklejenia dwóch
stożków podstawami wyraża się wzorem, niezależnie od tego, czy obracający się trójkąt będzie
prostokątny, czy nie:
| 1 | ||
V= | πr2x | |
| 3 |
| 20 | r | ||
= | |||
| 25 | 15 |
| 1 | ||
V= | *π*122*25=... | |
| 3 |