help
blogther:
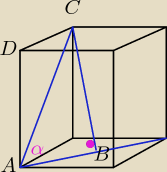
W graniastosłupie prawidłowym czworokątnym długość krawędzi podstawy jest równa 2a. Miara kąta
między przekątną podstawy a przekątną ściany bocznej wychodzącą z tego samego wierzchołka jest
równa . Oblicz objętość graniastosłupa.
AB = a
√2
czyli AD policze z twierdzenia pitagorasa
AD
2 = AC
2 − 4a
2
| | 2a2 − 4a2cos2α | |
AD2 = |
|
|
| | cos2α | |
| | 2a2(1 − 2(1−sin2α)) | |
AD2 = |
|
|
| | cos2α | |
| | 2a2(2sin2α − 1) | |
AD2 = |
| pierwiastkuje
|
| | cos2α | |
| | √(2sin2α − 1) | |
AD = a√2* |
|
|
| | cosα | |
| | √(2sin2α − 1) | |
V = 4√2a3 |
|
|
| | cosα | |
a odpowiedz jest to zadanie 6
http://operon.internetdsl.pl/arkusze_pm_2011/26_34523842309462364823475634534053/MATEMATYKA/matematyka_kryt_ocen_zak_roz.pdf
20 kwi 21:30
blogther: moze ktos mi wskazac gdzie popełniam bład
20 kwi 21:40
Aga1.: Prześledziłam Twoje rozwiązanie i błędu nie widzę.
Jedynie √cos2α=IcosαI=cosα, bo cosα>0
20 kwi 21:50
blogther: ta dwojka przy sin2α ona wszystko niszczy
20 kwi 21:52
kylo1303: 2sin
2α−1=sin
2α+sin
2α−1=sin
2α+1−cos
2α−1=sin
2α−cos
2α=−cos2α
Moze to cos pomoze, ale chyba nie
Jesli chodzi o trygonometrie to czesto dwa wygladajace na calkiem rozne liczby moga byc
tozsamosciowe. Wiec twoje rozwiazanie moze byc poprawne, mimo ze wyglada inaczej niz w
odpowiedziach.
20 kwi 22:27
blogther: okey dzieki za pomoc
20 kwi 23:09
Ania: AB = A √2 /2
24 lis 22:07