z gory dziekuje za pomoc Daniel: ZADANIE DLA EXPERTA Licze ze osoba ktora jest w stanie rozwiazac to zadanie jest w stanie rowniez mi je wytlumaczyc. Punkty będące srodkami okręgów stycznych zewnętrznie do okręgu o równaniu x²+y²=4 i jedoczesnie do osi OX tworzą pewien zbiór. Wyznacz ten zbior i narysuj go w ukladzie wspolrzednych. jedyne co umiem z tego zadania to wyznaczyc srodek i promien okregu o rownaniu x²+y²=4 S=(0,0) r=2

Daniel: brak expertow CÓŻ widze ze matematyka pisz upada .. jestem skazany na samodzielną męczarnie

kacper: Nic nie upada, tylko jest piątek popoludnie

Krzysiek: odległość od okręgu musi być równa odległości od prostej OX , spróbuj Sam napisać to równanie

Daniel: wiem wiem, juz zrobilem, troche wymęczyłem ale nic mi sie nie stało .. sorka nie wiedziałem ze dzis piątek

kacper: Nic nie szkodzi. Każdy czasem zapomina jakie dziś dzień

Eta: Byle przeżyć 9 maja ( dzień ......... zwycięstwa

MQ: Swoją drogą ciekawe rozwiązanie wychodzi: |y₀|=x₀²−25

Krzysiek: MQ , mi tam inne rozwiązanie wyszło

MQ: Jakie?

Krzysiek: |y|=1/4 x² −1

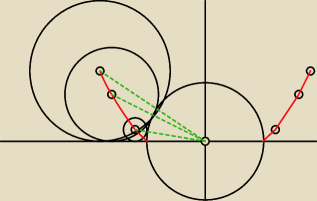
Skipper: ... i to samo pod osią Jeśli współrzędne środków oznaczysz x_s, y_s to ich odległość od środka danego okręgu będzie wynosiła √x_s²+y_s² i będzie jednocześnie równa 2+Iy_sI W rozwiązaniu otrzymasz parabolki

	xs2
ys=		−1 i odbicie ... oczywiście wszystko to w przedziałach (−∞, −2> i <2, ∞)
	4

MQ: Aaa, możliwe! Wziąłem okrąg o innym promieniu. Niemniej sama postać rozwiązania jest ta sama i całkiem ciekawa −− zwłaszcza jak ją się narysuje.