Obrót trójkąta Łukasz: Trójkąt o bokach długości równej 9 i 12 oraz kącie między tymi bokami o mierze 120 obraca się dookoła najdłuższego boku. Oblicz pole przekroju osiowego i objętość powstałej bryły. Policzyłem już wszytsko tylko zostało mi pole mam R dlugosci boków pole całego i długość C (przekątna AB jak z tego wyliczyć objętość? znaczy się skąd wziąć h?

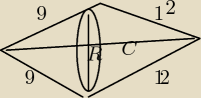
Łukasz: POLE CAŁEGO 54√3 R= 18√111/37 C=3√37 Jak policzyć mając te dane objętość bryły?

lucassky: proszę tylko o podpowiedz z pitagorasa chyba nie mam liczyc ? bo R jak podniose do kwadratu to nieciekawe wyniki wychodza

lucassky: help please

lucassky: jest może wzór na pole takiej figury bo wtedy H to byłoby c

lucassky: ?

Aga1.: c=H₁+H₂ c wyliczysz z twierdzenia cosinusów c²=12²+9²−2*12*9*cos120⁰ r wyliczysz ze wzoru na pole trójkąta

	1
P=		*12*9*sin1200
	2

	1
P=		c*h
	2

r=h trójkąta Pole przekroju to 2*pole trójkąta o bokach 12,9,c

	1		1		1		1
V=		πr2*H1+		πr2*H2=		πr2(H1+H2)=		πr2*c
	3		3		3		3

lucassky: chodziło mi tylko o obiętość czyli moge te wysokosci po prostu dodać i objętość całego to będzie 1/3πr²*c?

lucassky: wyszło dziękuje