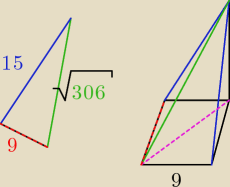
stereometria asdf: Podstawą ostrosłupa jest kwadrat. Wysokość ostrosłupa jest równa 12 cm, a jej spodek jest jednym z wierzchołków podstawy. Wiedząc, że V = 324, oblicz: a) P_c b) długość najdłuższej krawędzi bocznej. podpunkt b zrobiłem, z pierwszym podpunktem coś mam problemy Nie wiem jak wyznaczyć wysokość −−−−−−−−−−−−−−−−− 324 = 4 * a² a = 9

	1
Pc = 81 + 2*(9*12) *		+ 2* COŚ
	2

COŚ − pole trójkąta na obrazku, jakie jest jego pole?

Basia: 306 = 2*153 = 2*3*51 = 2*3*3*17 √306 = 3√34 masz wszystkie boki więc możesz skorzystać np. z wzoru Herona

Basia: albo tak: α kąt między bokami 15 i 9 z tw.cosinusów liczysz cosα z jedynki tryg. liczysz sinα (sinα>0)

	15*9*sinα
P =
	2

asdf:

	24 + 3√34
p =
	2

tak zostawić i liczyć? tw. cosinusów jeszcze nie miałem więc odpada Wzoru herona też nie miałem, ale wydaje mi się łatwiejszy, dzięki za pomoc.