trapez Madzia: jeżeli w trapezie mamy podana tylko wysokość to w jaki sposób obliczyć jego boki?

anmario: nie da rady, jak widzisz na rysunku, jedna wysokość H może być wysokością nieskończenie wielu różnych trapezów.

radek: gdyby ten trapez byl kwadratem to by sie dalo

Madzia: a jeżeli mamy w ten trapez wpisan okrąg i podaną jedynie wysokość?

anmario: Gdyby były podane wszystkie boki to wcale nie trzeba nic liczyć, nie? Gdyby

Madzia: hehe radek byłoby zbyt prosto

anmario: A to już insza inszość Madziu

Madzia: czyli?

anmario: Ale i tutaj jest nieskończenie wiele rozwiązań. Ujawnij jeszcze coś

radek: ee raczej sie nie da− co tu cudowac

Madzia: niestety nie wiem nic więcej:(

Madzia: chlopcy a potraficie takie zadanko? : W rownolegloboku o obodzie 40 cm przekatne sa dwusiecznymi katow, a ich długosci maja sie do siebie jak 3:4. Oblicz długości przekątnych tego rownolegloboku.

anmario: No to napisz "brak dostatecznej ilości danych" w odpowiedzi do tego zadania

anmario: Ja potrafię. Ale to chyba nie do mnie ten apel

Madzia: no okej mam nadzieje, ze nie bedzie z tego kosssy

radek: potrafie ale nie o tej godzinie

Madzia: do Ciebie również

Madzia: prosze

Madzia: no i chyba uciekli koledzy...

radek: w przecieciu przekatnych bedzie kat prosty cos czuje

radek: i cos z trojkatem bym pokombinowal

radek: ogolnie to te przekatne mozna zapisac ich dlugosci jako 3x i 4x

Madzia: własnie nie potrafię z obwodu wyliczyc dł. bokow

radek: ja sie poddaje

Madzia: kurcze...

Madzia: no coż dzięki za starania

Basia: Jeżeli przekątne równoległoboku są też dwusiecznymi to muszą być prostopadłe.

Madzia: czyli co to wnosi do zadania?

anmario: Ano twierdzenie Pitagorasa wnosi Madziu jeżeli tak jest rzeczywiście, czyli jeżeli są prostopadłe. A skoro Basia tak twierdzi to są. Reszta zadania jest w związku z tym dość prosta, poćwicz swoje możliwości.

Madzia: hmm moje możliwości matematyczne są niewielkie. Bez dł boków nie potrafię wyliczyć tego wszystkiego z pitagorasa..

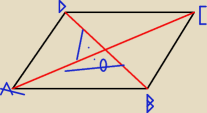
Basia: kąt BAD = kąt BCD = α kąt ABC = kąt ADC = 180−α kąt BAO = ^α₂ kąt ABO = ^180−α₂ = 90 − ^α₂ kąt BAO + kąt AOB + kąt ABO = 180 ^α₂ + kąt AOB + 90 − ^α₂ = 180 kąt AOB = 90 −−−−−−−−−−−−−−−−−−−−−−−−−−−− AB = CD = a BC = AD = b 2a + 2b = 40 a+b=20 −−−−−−−−−−−−−−−

BD		3
	=
AC		4

BD = 3x AC = 4x tr. AOB i tr.AOD są przystające bo: AO = AO BO = DO kąt AOB = kąt AOD = 90 czyli: AB = AD a=b Ob =4a = 40 a=10 czworokąt jest rombem

Basia: obeszło się bez Pitagorasa

Madzia: basiu dziękuje Ci bardzo i reszcie również za wielką pomoc

Basia: Tylko po co komu ta informacja o stosunku długości przekątnych ? Jesteś pewna Madziu, że dobrze przepisałaś treść zadania ?

Basia: A już wiem po co. Należy je obliczyć. I tu bez Pitagorasa już się nie obejdzie.

Madzia: Tak na pewno dobrze, w odpowiedziach mam, że powinno wyjść 12 i 16 cm.

Basia: A wiesz już jak policzyć długości tych przekątnych ?

Madzia: nie

Basia: AC = 4x BD = 3x AO = ^4x₂ = 2x BO = ^3x₂ z tw.Pitagorasa AB² = AO² + BO² 10² = 4x² + ^9x2₄ /*4 400 = 16x² + 9x² 400 = 25x² x² = ⁴⁰⁰₂₅ = 16 x = 4 AC = 4x = 16 BD = 3x = 12

Madzia: dziękuje bardzo Basiu już wszystko jasne tylko jedno pytanko, w tym zadaniu chyba te wszystkie obliczenia nie sa aż tak istotne? mozna czesc pominac?

Madzia: ok już łapię. Pozdrówka

Basia: nie można; wszystko po kolei musi być wykazane 1. przekatne przecinają się pod katem prostym ⇒ 2. tr.AOB i tr.AOD są przystające dopiero po wykazaniu tego masz prawo napisać: AB=AD = a Ob=4a=40 i dokończyć obliczenia

Madzia: dziękuje Basiu