stereometria asdf: Kąt rozwarcia stożka ma marę 60^o. Wykaż, że powierzchnia boczna stożka po rozwinięciu jest półkolem. P_b = 2πr³ Teraz który wzór trzeba użyć, żeby to wykazać?

asdf: pomoże ktoś?

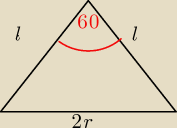
ewa: przekrój osiowy stożka jest więc Δrównobocznym. Zatem 2r=l P_b=πrl=πr*2r=2πr³ c.b.d.or

Mila: Wzór na p_b źle, popraw, uzależnij r od tworzącej. Trzeba zastosować wzór na wycinek koła.

	α
Pb=		*πl2
	360

asdf: Ewa, to samo wywnioskowałem z zadania, tylko jak udowodnić, że jest to półkole?

Basia: L = 2r β kąt wycinka koła o promieniu L

πL2		2π
	=
Pwycinka		β

π*4r2		2π
	=
2πr3		β

2π
	= 2
β

2π = 2β β = π czyli wycinek jest półkolem

ewa:

asdf: Racja Mila

	1
sin30o =
	2

l = 2r P_b = πrl P_b = 2πr², poprawiłem a teraz co?

	x
2πr2 =		* 2πr3
	360

nie rozumiem

asdf: Ok, dzięki za rozwiązanie, ale sam bym tego nie dowiódł

Basia: patrz post z 15:50 masz to rozpisane

ewa:

	1
Wystarczy pokazać że 2πr=		*2πl ( bo promień tego koła po rozwinięciu =l)
	2

A to wynika bezpośrednio z zależności l=2r

Basia: asdf nie mieszaj nigdy stopni z radianami; albo to, albo to

asdf: żebym ja wiedział co to radiany ok, dzięki robie kolejne zadanie

Basia: 2π to miara kąta pełnego w radianch π to miara kąta półpełnego w radianach itd. 1 radian = miara kąta, którego ramiona wycinają z okręgu o promieniu r łuk o długości L = r