trojkąty, patrycja: w trojkącie ABC poprowadzono cztery proste rownolegle do podstawy AB ,dzielące bok BC na pięć odcinkow rownej dlugosci. Suma dlugosci odcinkow tych prostych zawartych w trojkacie ABC jest o 10dm wieksza od podtsawy AB. Oblicz dlugosc boku AB. prosze o pomoc

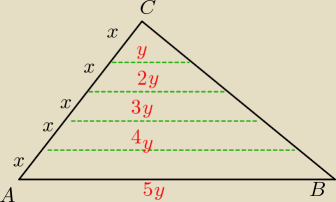
ewa: Rysunek zamieszczam, zaraz napiszę resztę

ewa: Suma tych zielonych prostych jest jak wynika z treści większa o 10dm od podstawy, czyli y+2y+3y+4y=5y+10dm To, że te zielone proste są równe y,2y,3y,4y i 5y wynika bezpośrednio z tw. Talesa Mamy zatem 10y=5y+10dm y=2dm AB=5y=10dm

Aga1.: IABI+10=x+y+z

x		y		z		AB
	=		=		=		//*w
w		2w		3w		4w

	y		z		AB
x=		=		=
	2		3		4

	AB
x=
	4

y		AB
	=		//*2
2		4

y=

z		AB
	=		//*3
3		4

z= Za x, y, z, podstaw do pierwszego równania i oblicz IABI.

Aga1.: IABI=20?

ewa: AC dzielimy Aga na 5 odcinków a nie na 4

Aga1.: ewa, masz rację, to ze mnie gapa.