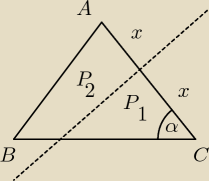
1.Dany jest trójkąt równoramienny ABC. ................: Mam ogromna prośbę Czy mógłby ktos pomóc mi 1.Dany jest trójkąt równoramienny ABC. Symetralna ramienia AC przecinając ramię BC rozcina ten trójkąt na dwie figury, których stosunek pól jest równy 1:2. Obliczyć tangens kąta przy wierzchołku C.

P(1)		1
	=
P(2)		2

................: POMOCY!

................: ?

ICSP:

MQ: Które ramiona są równe?

................: BA i AC

MQ: BCADE

MQ: ∡CBA = ∡BCA = α −− bo Δ równoramienny. ΔDCE i ΔDEA są przystające, więc pola ich są równe, więc pole ΔBDA też jest im równe. Stąd |BD|/|DC|=1/2 oraz ∡DCE = ∡DAE = α ΔABC i ΔACD są podobne, bo mają takie same kąty przy podstawach. Stąd: |DC|/|AC|=|AC|/|BC| ale |DC|=²₃|BC| stąd |BC|=|AC|*√3/√2 Niech |AC|=a, |BC|=b, a wysokość opuszczona z A na BC to h h dzieli |BC| na połowy, bo mamy trójkąt równoboczny. Mamy b=a*√3/√2 h²+(b/2)²=a² h²+a²*3/8=a² h²=a²*5/8 h=a*√5/(2√2) i na koniec tgα = h/(b/2)=(a*√5/(2√2))/(a*√3/(2√2))=√5/√3

MQ: Nie wyjaśniłem koncówki zdania: ΔDCE i ΔDEA są przystające, więc pola ich są równe, więc pole ΔBDA też jest im równe. pole ΔBDA jest równe polom ΔDCE i ΔDEA, bo pole BDEA = 2*ΔDCE, a pole ΔDEA jest równe polu ΔDCE Ponieważ pole ΔBDA jest dwa razy mniejsze od pola ΔDCA więc |BD|/|DC|=1/2