zadanie z ciągów
tn: Boki trójkąta prostokątnego są kolejnymi wyrazami ciągu arytmetycznego,
znajdź wszystkie takie trójkąty
O co tu chodzi?
19 kwi 22:16
tn: ?
19 kwi 23:12
Mila: a,a+r, a+2r boki Δprostokątnego
r>0
(a+2r)2=a2+(a+r)2
znajdź zależność r od a
Można boki inaczej oznaczyć.
19 kwi 23:21
Eta:
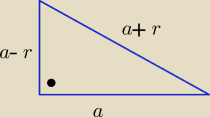
a>0 i r>0
z tw. Pitagorasa
a
2−2ar+a
2= a
2+2ar+r
2
a
2−4ar=0
a(a−4r)=0 ⇒ a=4r
mamy trójkąty o bokach: 3r, 4r, 5r
| | 3 | | 5 | |
Jest ich nieskończenie wiele np: (3,4,5 ) (6,8, 10) (15,20,25) ( |
| ,2, |
| ) |
| | 2 | | 2 | |
itd.................
19 kwi 23:46
tn: czyli jeśli boki trójkąta (dowolnego na razie) tworzą ciąg arytmetyczny to jest to dowód, że
jest prostokątny
20 kwi 07:21
Aga1.: Nie, w treści zadania musi być napisane,że jest prostokątny.
20 kwi 09:36