Problem z funkcją liniową Lukashem: Hej.Mam pytanie odnośnie funkcji. Wiadomo, że y = 3 jest funkcja liniową stałą, gdzie a = 0. Ale czy np. x = 3, też jest funkcją ? Dlaczego by nie ? przecież dziedzina jej to OY, a wartości leża na osi ox. Każdemu elementowi z dziedziny przyporządkowuję dokładnie jeden element ze zbioru OX. Wiec zdecydowanie to moim zdaniem jest funkcja , tylko Y −> X, a nie X − > Y. Dobrze myślę ?

krystek: x=3 nie jest funkcją ! prosta prostopadła do osi OY

krystek: OX ups

Ajtek: Jest tak jak napisałeś, jeżeli mielibyśmy X→Y, to nie będzie funkcja, jeżeli Y→X, wówczas jest to funkcja.

koło: Mnie w szkole uczono, że jeśli narysuję wykres funkcji i przecina się on w dwóch miejscach, gdy narysuję równoległą linie do osi OY, tzn. że nie jest to wykres funkcji Zauważ, że ani parabola, ani hiperbola i funkcje trygonometryczne itd. nie przecinają się w dwóch miejscach, gdy narysuję się pionową

krystek: y=ax+b a=tgα α=90 to tg90 nie istnieje!

Ajtek: krystek nie istnieje w odwzorowaniu X→Y, natomiast w odwzorowaniu Y→X będzie to funkcja, tak mi się przynajmniej wydaje.

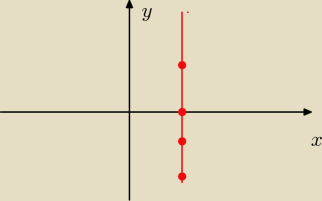
krystek: Jednemu x przyporządkowane nieskończenie wiele ygreków!

Ajtek: Ale w odwzorowaniu Y→X dla każdego y jest przyporządkowany dokładnie jeden x.

krystek: Tak @Ajtek w tym przypadku masz rację jeżeli mamy odwzorowanie z Y→X(jednemu y przyporządkowujemy jeden x)

Ajtek: O tym cały czas piszemy, nad tym się zastanawiamy .

krystek: Czytając uważnie Zadane pytanie brzmi: Czy x=3 jest funkcją? Odpowiadam NIE!

Ajtek: Początek tak, ale później następuje rozwinięcie do czego autor zmierzał . Oczywiście w odwzorowaniu X→Y x=3 nie jest funkcją .

b.: > Wiec zdecydowanie to moim zdaniem jest funkcja , tylko Y −> X, a nie X − > Y. > (...) w odwzorowaniu Y→X dla każdego y jest przyporządkowany dokładnie jeden x. Zgadza się! Problem powstaje z powodu użycia niedobrych oznaczeń, gdy pisze sie funkcje w notacji 'funkcyjnej', czyli po prostu f na funkcję, a f(x) na jej wartość w punkcie x, to problemu w ogóle nie ma.