p blogther: W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.

Eta: https://matematykaszkolna.pl/forum/85982.html

blogther: okey ale tam pisze ktory z walcow a my przeciez mamy tylko jeden wiec o co chodzi w tym poleceniu?

blogther: jak to jest z tym walcem przeciaz w wyniku tego obrotu mamy jeden tylko walec o co tu chodzi moze ktos wytłumaczyc?

blogther: czy po prostu policzyc pole i objetosc tego jednego walca?

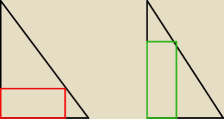
blogther: czyli w tym poleceniu chodzi o to ze jest wiele mozliwosci wpisana tego prostokata w ten trojkat tak? i mamy policzyc jaki walec powstały w ten sposob ma najwieksze pole tak?

kylo1303: Tak. A potem obliczyc jego objetosc.

blogther: tylko mam teraz taki problem bo P_b = 2πrh r = 2− y h = 4− x P_b = 2π( 2− y )(4− x) czyli teraz za P_b podstaiwm zero i moge sie pozbyc 2π bo to jest stałem i otrzymam cos takiego ( 2− y )(4− x)= 0 i musze to rozwiazac tak?

blogther: nie umiem tutaj doprowadzic do funkcji kwadratowej

blogther:

	2x − 8
wychodzi mi cos takiego y =		i teraz do wzoru Pb = 2π( 2− y )(4− x) musze
	x −4

wstawic za y to co wyliczyłem tak?

blogther: P_b = (2 − y)(4 − x) P_b =( 2 − ^2x−8_x−4)(x − 4) i licze tak?

blogther:

blogther: ale to bez sensu bo y = 2

kylo1303: Tzn ( 2− y )(4− x) to nie bedzie rownanie tylko funkcja, w ktorej musisz znalezc najwieksza wartosc. Jesli jest to funkcja kwadratowa to trzeba szukac w wierzcholku lub na granicach dziedziny. Jesli inna funkcja to juz zalezy od funkcji. Zaraz jak znajde chwile czasu postaram sie rozwiazac zadanie.

blogther: nie musisz ni tego rozwiazywac chce to zrobic sam

blogther: wydaje mi sie ze x∊(0;4)

kylo1303: Tzn ja nie bede tutaj pisac rozwiazania, bardzo dobrze ze sam starasz sie rozwiazywac bo na tym to wlasnie polega. Ale trudno jest pomagac "na sucho" (i nie chodzi tutaj o trunki). Jak zdolam rozwiazac to po prostu latwiej mi bedzie sie ustosunkowac do zadania.

kylo1303: A odpowiedz x∊(0,4) to co najwyzej moze byc dziedzina, bo odpowiedzia na pewno nie jest.

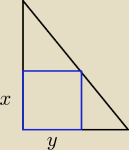
blogther: x∊(0;4) bo nie moze byc 0 i nie mowe byc wiekszy badz rowny 4 i tak samo z y y∊(0;2)

blogther: no tak

blogther: a moze cos z podobienstwa trojkatow trzeba wymyslic

blogther: no i bedziemy mieli ze x = 2y

blogther: ale mam racje ze to 2π mozemy pominac bo to jest stałe

kylo1303: Bardzo mozliwe ze trzeba. Pole boczne bedzie wynosilo P_b=2πxy . Kiedy to pole bedzie najwieksze? Musisz znalezc jeszcze jedno rownanie zeby uzaleznic y od x. I potem bedzie f. kwadratowa.

blogther: no i mam P_b = 2(2 − y)² z rozwiazanie układu x = 2y (2 − y)(4 − x)

kylo1303: A jak ci wyszlo ze x=2y ? I co ty oznaczasz za x i y? Boki prostokata czy czesc ktora zostanie na przyprostokatnych trojkata? Bo rysunek przedstawia pierwsza opcje a obliczenia druga.

blogther: x i y to sa boki prostokata

blogther: czyli zle bo teraz obliczam długosc tych odcinkow ktore nie sa długosciami prostokata

blogther: a juz sie cieszyłem ze mam dobrze

kylo1303: To wprawdz poprawki. Dodatkowo napisz skad ci sie wzielo x=2y.

kylo1303: Tzn nie mowie ze to zle (powiedzialbym nawet ze to jest dobrze), ale jakos nie widze skad to sie wzielo

blogther: 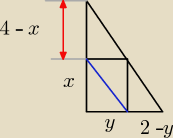^x_y = ⁴₂

kylo1303: Okej, ja po prostu korzystalem z innych proporcji Wyszlo w koncu?

blogther: x=2 y=1

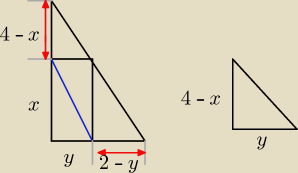
blogther: policzyłem to tak załozenia x∊(0;4) i y∊(0;2) z podbienstwa trojkatow

4−x		4
	=
y		2

4y = 8 − 2x | : 4 y = 2 − ^x₂ z podobienstwa trojkatow wyznaczyłem y ^x_y = ⁴₂ x = 2y rozwiazuje układ

⎧	y=x2
⎩	y = 2 − x2

^x₂ = 2 − ^x₂ x = 2 y = 1 czyli x i y spełniaja załozenia P_b = 2πrh x = 2 = h y = 1 = r P_b = 4π V = 2π czy moge to tak rozwiazac prosze o pomoc

blogther: jedynne do czego mozna sie doczepic to to ze policzyłem to dla konkretnego x i y wiec nie wiedomo czy to jest maksymalne pole czy minimalne

kylo1303: No wlasnie. Dlatego nie jest to dobre przedstawienie (poprawnego) rozwiazania. Pisalem ci wyzej ze: P_b=2πrh=2πxy . Zmiennymi sa x i y. Najwieksze pole jest wtedy, gdy xy jest najwieksze f(x)=xy oraz y = 2 − x/2 (wyszlo z podobienstwa). I teraz podstawiasz i liczysz f(max): y = 2 − x/2 (przeksztalce zeby bylo latwiej): 2y=4−x → x=4−2y=2*(2−y) f(x)=xy=y*(2−y)=−y²+2y

	−2
yw=		=1
	−2

y=1 to x=2

blogther: w ktorym trojkacie wyznaczyłes to podobienstwo

blogther: jak mogłbys wykonac rysunek bo przeciez bok 2 − y nie jest bokiem tego prostokata przynajmniej tak wynika z mojego rysunku no i ja wtedy z podobienstwa wyznaczyłem ze x = 2y i jak mamy ten wzor P_b = xy i jak podstaiwm za x = 2y to wychodziło mi P_b = 2y² nie wiem co robie zle przeciaz proporcja dobrze ułozona?

kylo1303: Nie jest dobrze wyznaczona. Zauwaz ze ten przekatna prostokata nie musi byc rownolegla z przeciwprostokatna. Dlatego tez x=2y jest blednym zalozeniem (tak w rzeczywistosci jest, bo boki prostokata to polowy odpowiednich bokow, ale nie mozemy tego zalozyc). Dlatego musisz skorzystac z tego co sam napisales:

4−x		4
	=
y		2

4−x=2y x=4−2y i to rownanie podstawic.

blogther: okey wielkie dzieki za pomoc

blogther: mam jeszce jedno pytanie jest jakies znaczenie czy wyznacze x czy y chodzi mi o to P_b = xy dla x = 4 − 2y P_b = y(4 − 2y) dla y = 8 − 2x P_b = x(8 − 2x) to jest bez roznicy tak?

kylo1303: Tzn jest to bez wiekszego znaczenie, po prostu wyznaczasz inny bok. Przy czym male zastrzezenia do zapisu powyzej: P_b=2πxy, a ty tylko upraszczasz sobie i liczysz f(max) funkcji f(x)=xy i y≠8−2x