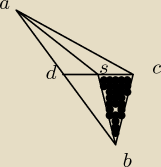
POMOCY - zawsze mam problem z wykazywaniem ..;/ Domiś: Odcinek CD jest środkową trójkąta ABC. Na odcinku CD wybrano dowolnie punkt S (S≠C i S≠D), a następnie poprowadzono odcinki AS i BS (rys). Wykaż, że pole trójkąta ASC jest równe polu trójkąta CSB.

MQ: Ponieważ CD to środkowa, to |AD|=|DB| W takim razie pola trójkątów ΔADC i ΔBDC są równe, oraz pola trójkątów ΔADS i ΔBDS są równe. Pole trójkąta ΔASC to pole ΔADC minus pole ΔADS Pole trójkąta ΔBSC to pole ΔBDC minus pole ΔBDS Ponieważ tamte parami były równe, więc te też są równe.

Domiś: dzięki