Bardzo proszę o pomoc, CocaCola: Trójkąt o boku długości a i kątach ostrych do niego przyległych o miarach \beta i \gamma obraca się dookoła prostej równoległej do tego boku, poprowadzonej przez wierzchołek kąta do niego przeciwległego. Oblicz objętość powstałej bryły.

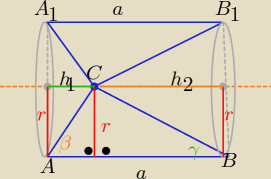
Eta: V(br)= V(walca ABA₁B₁ )− (V(stACA₁)+V(st BCB₁)) r_w=r(stożków) h_w= h₁(st)+h₂(st)= a

	1		2
V(br)= πr2*h −		πr2*h =		πr2*a=.....
	3		3

Wyznacz "r" ze wzoru sinusów =.........

elpe: dla Eta za taki rysunek

CocaCola: nie mogę wymyślić jak wyznaczyć "r"...

CocaCola: Eta ma wielki matematyczny talent

Eta: Dzięki

a		r
	=
sin[180o−(β+γ)]		sinβ

	a*sinβ
r=
	sin(β+γ)

CocaCola: właśnie miała napisać, że mi się udało, ale wielkie dzięki za pomoc I zadanko zrobione

CocaCola: pozdrawiam

Eta: Powodzenia na sprawdzianie

Dominik: troszke stare zadanie, ale odkopuje.

	2πa3sin2β
liczylem wszystko tak jak Eta i wychodzi mi V =
	3sin(β + γ)

w odpowiedziach objetosc ta jest wieksza o sin²γ (pomnozona). skad niby?

Dominik: w mianowniku oczywiscie jest sinus do kwadratu...

Dominik: jakies pomysly?

Dominik: znow podbijam

Dominik:

	asinβsinγ
r =
	sin(β + γ)

dalej sie zgadza z odp