W trójkącie ABC dane są: |AB|=c, kąt |CAB|= alfa ABC|=beta , gdzie beta>90 CocaCola: ETA, BASIA pomocy ! W trójkącie ABC dane są: |AB|=c, kąt |CAB|=α kąt ABC|=β , gdzie β>90 . Oblicz objętość bryły otrzymanej w wyniku obrotu trójkąta ABC wokół prostej zawierającej wysokość poprowadzoną z wierzchołka C.

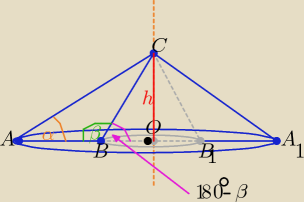
Eta: Bryła składa się ze stożka AA₁C i wydrążonego z niego stożka BB₁C o wspólnej wysokości "h" R −− dł. promienia podstawydużego stożka r −−− dł. promienia podstawy małego stożka |AB|=c R=c+r

	1
V(br) =		πh(R2−r2) =.......
	3

Spróbuj teraz policzyć ..........

CocaCola: ale jak wyliczyć (R²−r²) ...

CocaCola: chyba mam pomysł

CocaCola: udało się! dziękuje, dziękuję i jeszcze raz dziękuję

CocaCola: mam jeszcze jedno zadanie: Trójkąt o boku długości a i kątach ostrych do niego przyległych o miarach \beta i \gamma obraca się dookoła prostej równoległej do tego boku, poprowadzonej przez wierzchołek kąta do niego przeciwległego. Oblicz objętość powstałej bryły.