wielomiany Izabela: Pomóżcie 1. Dane są wielomiany W(x)=3x³+x²+1, P(x)=x+3 oraz Q(x)=x²−3. Wyznacz wielomian a) W(x)−P(x)*Q(x) b) W(x)*P(x)−Q(x) 2. Rozłóż wielomian na czynniki W(x)=6x³+48 3. Rozwiąż równanie i nierówność x³+5x=x+5 x(3x−1)(x+3)(x−3)(2+x)>0

Eta: Podpowiadam

Izabela: tak

Eta: 1/ podstaw i wykonaj działania: a) 3x³ +x² +1 −( x+3)((x² −3)= ......... b ) (3x³ +x² +1)((x+3) − ( x² −3)= ........... wykonaj działania i zredukuj wyrazy podobne i to wszystko! zad2/ 6x³ +48= 6( x³ +8) = ....... zastosuj wzór : a³ +b³ = (a +b)( a² − ab +b²) gdzie a = x b = 2 zad3/ a) x³ +4x − 5 =0 x³ − x² +x² − x +5x − 5=0 x²( x −1) +x(x−1) +5( x −1)=0 (x −1) ( x² +x +5)=0 Δ= −19 −− brak pierwiastków w drugim wyrażeniu więc jedynym rozwiązaniem jest x = 1 b) masz gotowy rozkład na czynniki więc m−ca zerowe to: x = 0 x= ¹₃ x = − 3 x = 3 x = −2 Zaznacz na osi liczbowej poprowadź taką falistą krzywą przez wszystkie miejsca zerowe zaczynając od góry po prawej stronie przez wszystkie te miejsca jako odp; podaj przedziały tych części wykresu z nad osi OX

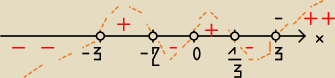
Eta: Odp: do ostatniego zad: x€( (−3, −2) U ( 0,¹₃) U ( 3, ∞)

Izabela: Eto dzięki za pomoc ale czy możesz sprawdzić czy dobrze obliczyłam Zad 1. a) =2x³−2x²+9x+10 b) = 3x⁴+10x³+2x²+x+6 Zad 2. x³+2³=(x+2)(x²−2x+2²) czy to już wszystko o tego zadania bo przyznam się szczerze nie wiem Zad 3. dziękuję

Izabela: zad 3 x3 − x2 +x2 − x +5x − 5=0 a skąd to się wzięło

Izabela: błąd x³−x²+x²−x+5x−5=0

Izabela: czy może ktoś sprawdzić te moje wyniki

rzekomy: wszystkook

Izabela: czyli na pewno te zadania są ok a czy może mi ktoś wytłumaczyć skąd się to wzięło x³−x²+x²−x+5x−5=0 w 3 zadaniu

Izabela: proszę o sprawdzenie

Izabela: czy ktoś mi pomoże, proszę

Izabela: :(

Mickej : x³+5x=x+5 x³−x+5x−5=0 x(x²−1)+5(x−1)=0 x(x−1)(x+1)+5(x−1) przed wyrażenie wyciągamy całe x−1 (x−1)[x(x+1)+5]=0 jedno miejsce zerowe to 1 a reszte liczymy z kwadratowego nawiasu x(x+1)+5=0 x²+x+5=0 Δ=1−20 Δ<0 więc jedyne rozwiązanie to x+1 ostateczna postać może wyglądać tak (x−1)(x²+x+5)=0

Izabela: wielkie dzięki a czy mógłbyś sprawdzić jeszcze moje wyniki do zad 1 i 2 Zad 1. a) =2x³−2x²+9x+10 b) = 3x⁴+10x³+2x²+x+6 Zad 2. x³+2³=(x+2)(x²−2x+2²) czy to już wszystko o tego zadania bo przyznam się szczerze nie wiem