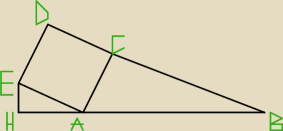
Trójkątyy Pomocy proszę: Proszę o pomoc, wskazówkę. Nie umiem tego zrobić Na zewnątrz trójkąta prostokątnego ABC, w którym kąt |ACB|=90 oraz |AC|=5 |BC|=12 zbudowano kwadrat ACDE. Punkt H leży na prostej AB i kąt |EHA|=90. Oblicz pole trójkąta HAE.

Pomocy proszę: proszę o naprowadzenie ; /

Jacek Karaśkiewicz: Oznaczmy: miara kąta CAB − α miara kąta CBA − β miara kąta EAH − γ miara kąta HEA − δ miara kąta EAC − Δ α + β = 90^o ⇒ β = 90^o − α γ = 180^o − Δ − α = 90^o − α = β δ = 180^o − 90^o − γ = α Czyli mamy γ = β i δ = α. A więc trójkąty CAB i EHA są podobne. |EA| = |AC| = 5 |AB| = √5² + 12² = 13

	5
Czyli podobieństwo jest w skali		.
	13

S_CAB = ¹₂ * 5 * 12 = 30

	5		25		750
SEHA = SCAB * (		)2 = 30 *		=
	13		169		169

Jeśli się gdzieś pomyliłem, to proszę o poprawienie.

tim: Kąt CAB ma α Kąt CAE ma 90 Kąt EAH ma 180 − 90 − α = 90 − α Kąt AEH ma 180 − 90 − 90 + α = α Trójkąty EHA oraz ACB są podobne K, K, K. EHA, ACB EAH, CBA AEH, CAB <−−−−−− Kąty identyczne (3 pary) Skoro przyprostokątne są podobne w skali (k) = 13/5 = 2,6 Pole ich będzie podobne k² = 6,76 Pole ABC = 30 Pole EHA = 4 74/169

tim: Jacku dobrze

Pomocy proszę: Dziękuję Wam bardzo dla mnie to zadanie było mega trudne..dziekuje raz jeszcze

lll: