wyznacz dziedzine funkcji blogther: wyznacz dziedzine funkcji y = √x³ − 3x² − 4x + 12 + log_5−x(^x−2₅ + ^2x−4₅ +^{3x −6}₅ +...+^10x−20₅) zapisałem to tak D_f={x³ − 3x² − 4x + 12≥0∧5−x≠1∧5−x>0∧^x−2₅+^2x−4₅+^{3x −6}₅+...+^10x−20₅>0} i wyszło mi ze D_f=<2;5) dobrze?

blogther: moze ktos pomoc

Rafał274: Jeśli chodzi o logarytm całe wyrażenie to :

	x−2
(1 + 2 + 3 + ... + 10) *		= 11(x−2)
	5

11(x−2) > 0 x ∊ <3; 4) ∪ (4; 5)

Rafał274: + pozostałe warunki oczywiście

blogther: skad wzieła Ci sie ta czworka?

blogther: ja mam taka odpowiedz teraz x∊<3;5) u {2} ale czy ta dwojka tez ma byc to nie jestem pewny

blogther: mamy podac czesc wspolna takich warunkow D_f={x−3)(x−2)(x+2)≥0 ⋀ x≠5 ⋀ x>5 ⋀ x>2}

blogther: pomoze ktos?

Rafał274: Jeszcze raz : x³ − 3x² −4x + 12 ≥ 0 (x − 2)(x + 2)(x − 3) ≥ 0 x ∊ <−2; 2>∪<3; +∞) 5 − x > 0 ⋀ x ≠ 4 ⇔ x ∊ (−∞; 4) ∪ (4; 5) 11(x−2) > 0 ⇔ x∊(2; +∞) Czyli iloczyn tych zbiorów to : <3; 4)∪(4; 5)

Rafał274: 5 − x ≠ 1 (podstawa logarytmu) x ≠ 4

blogther: a tej dwojki nie uwzgledniamy tak?

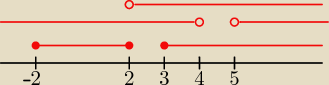
Rafał274: Najmniejszą liczbę wszystkie trzy przedziały mają dopiero 3.

mały: f(x) = 2x−log(−10x+20)

ZKZ: Z definicji logarytmu log_a b=c gdzie a>0 i a nie =1 i b>0 to dalej Ty