rozwiaz nierownosc wymierna olek: x²+4x+4/x²−4>0

asdf: tak o:

x2 + 4x + 4
	> 0
x2 − 4

Dorotaz: dziedzina x∊ R\{−2,2} x²+4x+4 > 0 Δ=16−16 > 0

	−4
x0=		> −2
	2

x∊ (−∞,−2) v(−2,+∞) nie jestem pewna, ale chyba tak

Dorotaz: o odpowiedz chyba inna (−∞, −2)v(−2,2)V{2,+∞) cos namieszałam chyba

Jolanta:

x2+4x+4
	>0 x2−4≠0
x2−4

(x+2)(x−2)≠0 x≠−2 x≠2 (x²+4x+4)(x²−4)>0 (x+2)²(x²−4) jezeli nie widzisz,że mozna skorzystać ze wzoru (a+b)² liczysz Δ Δ=16−16=0

	−b		−4
x=		=		=−2
	2a		2

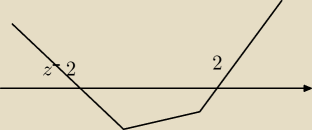
x²+4x+4=(x+2)(x+2) (x+2)(x+2)(x+2)(x−2)> zaczynam rysować od prawej strony nad osia x bo a>0 przecinam os x=2 idę pod osią do x=−2 x=−2 jest pierwiastkiem trzykrotnym czyli nieparzystym wiec wykres przechodzi(przy parzystych nastepuje odbicie) x∊(−∞,−2)v(2,∞)

MQ: Wzięłaś pod uwagę tylko przypadek, kiedy x²−4>0 Musisz jeszcze rozpatrzyć przypadek, kiedy x²−4<0

Jolanta:

	a
tak mnie uczyli		>0 jezeli a*b>0
	b

a>0 i b>0 to a*b>0 a<0 i b<0 to a*b>0

Jolanta: Moze ktoś sie wyjaśnić ?

krystek:

(x+2)2
	>0
x+2)(x−2)

(x+2)³(x−2)>0⇒x∊(−∞,−2)U(2,∞) a jak inaczej?

Jolanta: MQ miał jakies wątpliwości co do mojego rozwiązania

krystek: Nie wiem o co MQ chodziło ,' Może się odezwie.