równania lisa: Pierwiastkami równania x²+bx+c=0 są liczby −6 i 2. Wyznacz wartość parametrów b i c. układ równań: (−6)²+6b+c=0 2²+2b+c=0

Patryk: lepiej tak (x+6)(x−2) i porónujesz

Patryk: wymnozyc trzeba

krystek: w pierwszym błąd −6b

lisa: no wiem.Już pod koniec wychodz mi taki układ równań : 36+6b+c=0 −4−2b−c=0 .

krystek: 36−6b+c=0

asdf: 36 + 6b + c = 0 4 + 2b + c = 0 32 + 4b = 0 4b = −32 b = −8 podłóż i zrób

asdf: poprawka: 36 − 6b + c = 0 4 + 2b + c = 0 32 − 8 b = 0 −b = −32 b = 4

lisa: ok dzięki Jeszcze jakbyś mógł mi powiedzieć czy w funkcjach trygonometrycznych jak mamy wartość np. sin ¹_√21 to uwymierniamy czy zostawiamy w takiej formie?

lisa: w mianowniku jest pierwiastek

asdf: daj treść

lisa: nie chodzi o treść tylko o zasadę.

asdf: to zależy, odpowiadając na zadanie "oblicz wartość sinx", a w wyliczeniach wychodzi Ci:

	1		√21
sinx =		to podajesz sinx =
	√21		21

Najlepiej podaj treść przykładowego zadania, bo czasem nie warto tego robić a czasem warto, a teraz nie chce Tobie namotać.

krystek: Usuwasz niewymierność!

lisa: No tylko o to mi chodziło Nie byłam pewna czy w ogóle sie uwymiernia. Dziękuję ślicznie

krystek: Ok! Ale określenie ?! Usuwam niewymierność z mianownika − czyli "uwymierniam"?

lisa: yyyy moja kobieta od matematyki tak mówi ale czy jest w pełni kompetentna to kwestia zastanowienia tak jpowyższe określenie

krystek: Ciekawe , całe życie człowiek się uczy i zawsze czegoś nie wie.

lisa: Jedyne co wiemy to to że nic nie wiemy jak mawial Sokrates

krystek: Powodzenia!

krystek: Ale co do Twojego zadania , szybciej miałabyś ,gdybyś postać iloczynową zastosowała jak podał Patryk o 19:27

lisa: hahaha

lisa: ale moja kobieta od matematyki moglaby mi tego nie uznac jeżeli nnie robie sposobem jaki ona podała

asdf: To gratuluje nauczyciela z matematyki.

lisa: Także tego... Na jutro 50 zadań i upragniony koniec

asdf: roku czy szkoły?

lisa: Szkoły. Matura w tym roku

lisa: Szkoły. Matura w tym roku

krystek: Trudno uwierzyć ,ale spotkałam się już z takimi n−lami nie uznającymi innych sposobów.

lisa: ja mam swoją teorię na ten temat, ale nie wygłoszę jej publicznie hehe

krystek:

lisa: teoria spiskowa dziejów.

seq12345: liczby −3 i 4 sa pierwiastkami równania 2x²+bx+c=0 wyznacz współczynniki b i c

seq12345: dana jest funkcja f(x)=a(x−4)²+3 ktorej wykres przecina os y w punkcie P(0,−5) oblicz wspolczynnik "a" , wspolrzedne wierzcholka , podaj rownanie osi symetrii tej paraboli

Mila: 1) dla seq12345 2(x+3)(x−4)=2x²+bx+c⇔porównamy współczynnik 2(x²−4x+3x−12)=2(x²−x−12)=2x²−2x−24 ⇔ 2x²−2x−24=2x²+bx+c⇔ b=−2, c=−24 spr. Δ=4+4*2*24=196

	2−14		2+14
x1=		=−3 lub x2=		=4
	4		4

Dominik: mozna tez z wzorow viete'a

c
	= −3 * 4
2

−b
	= −3 + 4
2

c = −24 b = −2 2x² − 2x − 24.

Mila: 2) dla seq12345 f(x)=a(x−4)²+3 ktorej wykres przecina os y w punkcie P(0,−5) f(0)=−5⇔a(0−4)²+3=−5 16a=−8

	1
a=−
	2

	−1
f(x)=		(x−4)2+3
	2

b) wsp wierzchołka paraboli (p,q)=(4,3)⇔x_w=4,y_w=3 c)x=4 oś symetrii paraboli ( pierwsza wsp. wierzchołka) Zakładaj nowe wątki, nie dopisuj się do starych.

seq12345: dana jest funkcja f(x)=a(x+1)²+4 ktory wykres przecina os y w punkcie P(0,−2) oblicz wspolczynnik "a" , wsp wieszcholka podaj rownanie osi symetrii to samo dal 2 grupy podstawilem jak w 1 ale nie wiem czy dobrze xD

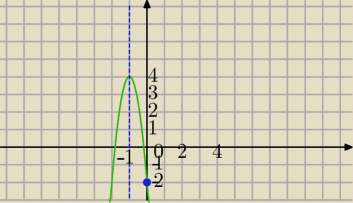
Mila: f(x)=a(x+1)²+4 ktory wykres przecina os y w punkcie P(0,−2) f(0)=−2⇔a(0+1)²+4=−2 a+4=−2 a=−6 f(x)=−6(x+1)²+4 x_w=−1 y_w=4 x=−1 oś symetrii paraboli