Oblicz długości przekątnych i pole tego równoległoboku Agnieszka: W równoległoboku ABCD |AB|=10 |AD|=6.Odległość wierzchołka D od BC wynosi 6

M:

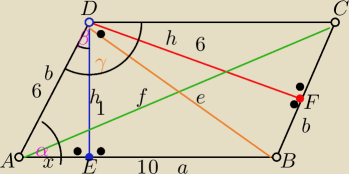
Bo_ra: AB=CD=a=10 AD=BC=b=6 DF=h=6 DE=h₁=? AE=x=? ∡DAE=α=? ∡ADE=β=? γ=β+90^o P=BC*DF P=b*h=6*6=36j² =============== P=AB*DE P=a*h₁

	36
h1=		=3,6 jm
	10

================= AE=x=√AD²−h₁² x=√6²−3,6)²=4,8

	x		4,8
cosα=		=		=0,8
	b		6

e²=a²+b²−2a*b*cosα e²=10²+6²−2*10*6*0,8 e²=136−96=40 e=√40=2√10

	h1
cosβ=
	b

	3,6
cosβ=		=0,6
	6

β=53^o γ=53⁰+90⁰= 143^o cos143^o=−sin53^o −sin53^o=−0,7986 f²=b²+a²−2*b*a*cos143^o f²=6²+10²−2*6*10*(−0,7986) f²= 136+95,832=231,832 f=15,23

baba raba: P=6*6=36 w trójkącie prostokątnym DEC : |EC|=8 to |EB|=2 z tw. Pitagorasa wΔDEB : e²=36+4 ⇒ e=2√10 w kazdym równoległoboku zachodzi : f²+e²=2a²+2b² to f²= 200+72−40 ⇒ f= 2√58