. california-: W sześcianie o krawędzi długości a połączono środki S1, S2 i S3 trzech krawędzi wychodzących z wierzchołka D1 i otrzymano trójkąt S1S2S3. Oblicz jego pole P.

Ajtek:

	a√2
Jest to Δ równoboczny, o boku dł.
	2

california-: to właśnie już obliczyłam chciałam sie tylko upewnić co do wyniku. bo nie jestem pewna czy dobrze policzyłam

Ajtek: To teraz licz pole .

biga: skąd wam ten wynik wyszedł?

Mila:

	a		a
e2=(		)2+(		)2
	2		2

	a2		a2		a2
e2=		+		=
	4		4		2

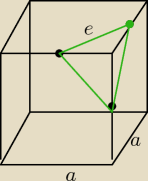
Δ jest równoboczny

	e2√3		a2		√3		a2√3
PΔ=		=		*		=
	4		2		4		8

Patrycja: jak obliczyliście ten bok O_o

Patrycja: bo nie rozumiem

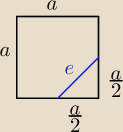
dero2005: (^a₂)² + (^a₂)² = e^{2 a2}₄ + ^a2₄ = e²

a2
	= e2
2

	a√2
e =
	2