Trójkąt prostokątny
Katej:
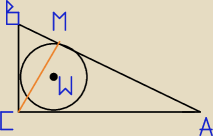
Dany jest trójkąt ABC w którym |BC|=30, |AC|=40, |AB|= 50.
Punkt W jest srodkiem okręgu wpisanego w ten trójkat.
Okrąg wpisany w trójkat ABC jest styczny do boku AB w punkcie M.
Oblicz długośc odcinka CM.
Może mnie ktoś naprowadzić jak rozwiązać to zadanie? Proszę.
19 kwi 11:53
imię lub nick: | | |AC|*|BC| | |
ze wzoru na wysokość w trójkącie prostokątnym: |
| =|CM| |
| | |BA| | |
19 kwi 11:58
imię lub nick: chyba

19 kwi 12:00
Katej: Dziękuję

19 kwi 12:02
viola: To nie jest wysokość
19 kwi 12:03
Katej: Zastanawia mnie właśnie to bo odcinek |CM| nie przechodzi prez punkt W
19 kwi 12:05
Mickej : na bank to nie jest wysokość trzeba skorzystać z promienia tego oktęgu
19 kwi 12:07
viola: r=P/p p−połowa obwodu P pole trójkąta
p=60 P=600 r=10
BM=20 M punkt styczności okręgu i przeciwprostokątnej
19 kwi 12:10
Mickej : narysuje co trzeba
19 kwi 12:10
imię lub nick: zasugerowałem się rysunkiem.. ehh
19 kwi 12:11
viola: ale wysokość się też przyda, zrób sobie porządny rysunek.
19 kwi 12:11
Katej: kąt CMA na ryskunku nie jest kątem prostym
19 kwi 12:14
Mickej :
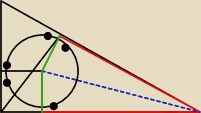
te czarne kropki to kąty proste r wyznaczasz z tego co ci viola napisała czerwone proste
są równe które równają się bok CA−r a dalej to ja bym liczył na kątach albo z
twierdzenia cosinusów
19 kwi 12:16
Mickej : te kąty proste są przy promieniu a nie przy tej prostej poprowadzonej do stycznej
19 kwi 12:17
Katej: To chyba jednak dla mnie za trudne ; /
Dziękuję za podpowiedzi ; )
19 kwi 12:24
Katej: Jest może prostsza metoda rozwiązania tego zadania?: /
Jak tak to prosze o pomoc ; /
19 kwi 12:36
viola: CM i wysokość są bokami trójkąta prostokątnego , jak masz wysokość h=(30*40)/50 to
mozesz obliczyć odcinek między wierzchołkiem B i wysokością (oznaczenia z Twojego
rysunku)
19 kwi 12:55
Bogdan:
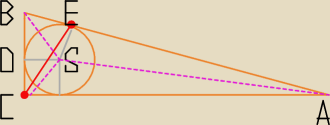
|BC| = 30, |AC| = 40, |AB| = 50
|CD| = |DS| = |SE| = r − długość promienia okręgu wpisanego,
S − środek okręgu wpisanego, punkt przecięcia dwusiecznych kątów wewnętrzych,
r =
12(30 + 40 − 50) = 10
Trójkąty BDS i BES są przystające
|DB| = |EB| = 30 − 10 = 20
|<CBE| = |<CBA| = α, cosα =
3050 = u{3}[5}
Mamy obliczyć |CE|.
Korzystamy z wzoru kosinusów w trójkącie BCE:
|CE|
2 = 30
2 + 20
2 − 2*30*20*
35
Po wykonaniu obliczeń otrzymamy |CE|
19 kwi 13:37
Katej: Dziękuję bardzo bardzo, jeszcze raz. ;−)
19 kwi 14:10
 Dany jest trójkąt ABC w którym |BC|=30, |AC|=40, |AB|= 50.
Punkt W jest srodkiem okręgu wpisanego w ten trójkat.
Okrąg wpisany w trójkat ABC jest styczny do boku AB w punkcie M.
Oblicz długośc odcinka CM.
Może mnie ktoś naprowadzić jak rozwiązać to zadanie? Proszę.
Dany jest trójkąt ABC w którym |BC|=30, |AC|=40, |AB|= 50.
Punkt W jest srodkiem okręgu wpisanego w ten trójkat.
Okrąg wpisany w trójkat ABC jest styczny do boku AB w punkcie M.
Oblicz długośc odcinka CM.
Może mnie ktoś naprowadzić jak rozwiązać to zadanie? Proszę.


 te czarne kropki to kąty proste r wyznaczasz z tego co ci viola napisała czerwone proste
są równe które równają się bok CA−r a dalej to ja bym liczył na kątach albo z
twierdzenia cosinusów
te czarne kropki to kąty proste r wyznaczasz z tego co ci viola napisała czerwone proste
są równe które równają się bok CA−r a dalej to ja bym liczył na kątach albo z
twierdzenia cosinusów
 |BC| = 30, |AC| = 40, |AB| = 50
|CD| = |DS| = |SE| = r − długość promienia okręgu wpisanego,
S − środek okręgu wpisanego, punkt przecięcia dwusiecznych kątów wewnętrzych,
r = 12(30 + 40 − 50) = 10
Trójkąty BDS i BES są przystające
|DB| = |EB| = 30 − 10 = 20
|<CBE| = |<CBA| = α, cosα = 3050 = u{3}[5}
Mamy obliczyć |CE|.
Korzystamy z wzoru kosinusów w trójkącie BCE:
|CE|2 = 302 + 202 − 2*30*20*35
Po wykonaniu obliczeń otrzymamy |CE|
|BC| = 30, |AC| = 40, |AB| = 50
|CD| = |DS| = |SE| = r − długość promienia okręgu wpisanego,
S − środek okręgu wpisanego, punkt przecięcia dwusiecznych kątów wewnętrzych,
r = 12(30 + 40 − 50) = 10
Trójkąty BDS i BES są przystające
|DB| = |EB| = 30 − 10 = 20
|<CBE| = |<CBA| = α, cosα = 3050 = u{3}[5}
Mamy obliczyć |CE|.
Korzystamy z wzoru kosinusów w trójkącie BCE:
|CE|2 = 302 + 202 − 2*30*20*35
Po wykonaniu obliczeń otrzymamy |CE|